Tổng hợp các câu hỏi khó phần Đại số trong đề thi Toán vào 10 Sở Hà Nội năm 2025

Từ hình vuông có cạnh bằng 6 bạn An cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó bạn An gập thành hộp quà có dạng hình hộp chữ nhật không nắp. Tìm x để thể tích của hộp quà là lớn nhất.

Trả lời: x = .

Người ta thiết kế một thùng chứa hình trụ có thể tích V nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỷ số sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất?  

Trả lời: = .

Bác An có một mảnh vườn hình vuông cạnh 4 m. Ở bốn góc vườn, bác An muốn trồng hoa vào các hình tam giác vuông bằng nhau (xem hình vẽ). Hãy tính khoảng cách từ góc vườn A đến vị trí E sao cho phần còn lại của mảnh vườn là tứ giác EFGH có chu vi nhỏ nhất. 

Trả lời: AE = m.

Người ta muốn dùng một tấm bạt hình chữ nhật dài rộng để phủ kín mái và hai mặt trái, phải của một cái lều dài. Biết hai mái lều là các hình chữ nhật bằng nhau và hợp với nhau tạo thành góc vuông (hình vẽ). Tính độ cao h của cột lều để thể tích cái lều lớn nhất. (kết quả làm tròn đến hàng phần trăm)

Trả lời: Chiều cao cột lều h ≈ m thì thể tích cái lều lớn nhất.

Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8 000 quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ. Tìm số máy móc công ty nên sử dụng để chi phí sản xuất 8 000 quả bóng là thấp nhất.

Trả lời: Công ty nên sử dụng máy để chi phí sản xuất là thấp nhất.

Một thợ cơ khí cắt vừa đủ một cây sắt dài 100 dm thành các đoạn để hàn lại thành khung của một hình lập phương và một hình hộp chữ nhật. Biết hình hộp chữ nhật có chiều dài gấp 6 lần chiều rộng và chiều cao bằng chiều rộng. Tìm độ dài của các đoạn cắt sao cho tổng thể tích của hai hình thu được nhỏ nhất?

Trả lời: Để tổng thể tích của hai hình thu được nhỏ nhất, ta cần cắt cây sắt thành 6.1 đoạn có độ dài 3 dm để hàn thành khung hình lập phương; 6.2 đoạn 2 dm và 6.3 đoạn 12 dm để hàn thành khung hình hộp chữ nhật.

Người ta muốn rào quanh một khu đất với tổng chiều dài là a (m) thẳng hàng rào. Ở đó người ta tận dụng một bờ tường có sẵn để làm một cạnh của hàng rào. Vậy để rào khu đất ấy theo hình chữ nhật sao cho có diện tích lớn nhất thì giá trị lớn nhất đó tính theo a bằng:

Độ giảm huyết áp của một bệnh nhân được cho bởi công thức: f(x) = 0,025x²(30 - x), trong đó x (miligam) là liều lượng thuốc được tiêm cho bệnh nhân. Khi đó, liều lượng thuốc nhiều nhất được tiêm cho bệnh nhân để huyết áp giảm là bao nhiêu?

Trả lời: Liều lượng thuốc nhiều nhất được tiêm cho bệnh nhân là miligam.

Người ta cần làm một cái bồn chứa dạng hình trụ có thể tích 1000 lít bằng inox để chứa nước, tính bán kính đáy R của hình trụ đó sao cho diện tích toàn phần của bồn chứa đạt giá trị nhỏ nhất. (Diện tích toàn phần bằng tổng của diện tích xung quanh và diện tích hai đáy)

Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ.

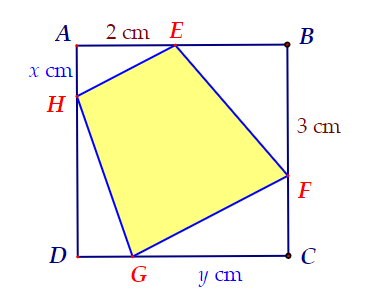
Tìm tổng x + y để diện tích hình thang EFGH (S_EFGH) đạt giá trị nhỏ nhất.

Chi phí cho xuất bản x cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, giấy in...) được cho bởi công thức:  (đơn vị: vạn đồng). Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số  với T(x) là tổng chi phí (xuất bản và phát hành) cho x cuốn tạp chí, được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản x cuốn. Chi phí trung bình cho mỗi cuốn tạp chí thấp nhất là bao nhiêu?

Trả lời: Chi phí trung bình cho mỗi cuốn tạp chí thấp nhất là đồng.

Cho một tấm nhôm hình tam giác đều có cạnh bằng 20 (cm). Người ta cắt ở ba góc của tấm nhôm đó ba tam giác nhỏ để được hình chữ nhật MNPQ. Tìm độ dài đoạn MB để hình chữ nhật MNPQ có diện tích lớn nhất.

Trả lời: MB = cm.

Với một miếng tôn hình tròn có bán kính bằng R = 6 cm. Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (Như hình vẽ). Hình nón có thể tích lớn nhất khi độ dài cung tròn của hình quạt được gấp thành hình nón bằng bao nhiêu?

Cho một tấm nhôm hình chữ nhật ABCD có AD = 60 cm, AB = 40 cm. Người ta gập tấm nhôm theo hai cạnh MN và PQ vào phía trong cho đến khi AB và DC trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy. Khi đó, để tạo được khối lăng trụ có thể tích lớn nhất thì giá trị của x phải bằng bao nhiêu?

Trả lời: x = cm.

Bác Sơn muốn xây một bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích bằng 36 m³. Đáy bể có dạng hình chữ nhật với chiều rộng là x (m), chiều dài gấp đôi chiều rộng. Bác Sơn muốn phần diện tích cần xây (bao gồm diện tích xung quanh và đáy bể) là nhỏ nhất để tiết kiệm chi phí thì x phải bằng bao nhiêu?

Trả lời: x = m.

Ông Bình có 24 m rào thép B40. Ông Bình muốn rào một mảnh vườn hình chữ nhật bằng cách tận dụng một cạnh của vườn là một bức tường dài (hình vẽ), chỉ có ba mặt là rào thép B40. Hỏi ông Bình cần rào mảnh vườn hình chữ nhật có kích thước là bao nhiêu để diện tích mảnh vườn là lớn nhất?

Trả lời: Mảnh vườn có chiều dài 16.1 m và chiều rộng 16.2 m.

Ngày xưa có một vị tể tướng nổi tiếng thông thái. Đến khi tể tướng muốn cáo quan về quê, nhà vua liền ban thưởng bằng cách đưa cho tể tướng một cuộn dây dài 400 mét và nói: “Ngươi hãy căng sợi dây này thành một hình chữ nhật, sao cho hai đầu dây chạm vào nhau. Mảnh đất bên trong hình chữ nhật đó sẽ thuộc về ngươi". Hỏi tể tướng sẽ căng sợi dây như thế nào để mảnh đất có diện tích lớn nhất?

Trả lời: Tể tướng sẽ căng sợi dây thành 17.1hình vuônghình chữ nhậthình thoi có cạnh 17.2 m.

Một người nông dân chuẩn bị 15 000 000 đồng cho việc làm một hàng rào hình chữ E dọc theo bờ sông để tạo thành một khu đất trồng rau có hai ô hình chữ nhật như nhau có kích thước như hình vẽ. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng một mét rào, còn đối với ba mặt hàng rào còn lại thì chi phí nguyên vật liệu là 50 000 đồng một mét rào. Tìm x và y để diện tích đất trồng rau thu được là lớn nhất.

Trả lời: x = 18.1 m; y = 18.2 m. (Kết quả viết dưới dạng số thập phân nếu số không nguyên)

Để làm một chiếc máng thoát nước, người thợ từ 1 tấm tôn hình chữ nhật kích thước 1 m x 40 cm, đánh dấu 2 đường chia và gò lại thành 1 chiếc máng có dạng hình hộp chữ nhật (thiếu mặt đáy trên và 2 mặt bên) như hình vẽ. Em hãy giúp người thợ tìm giá trị của x (đơn vị cm) để thể tích máng thoát nước là lớn nhất.

Trả lời: x = cm.

Một bức tường cao 2 m nằm song song với tòa nhà và cách tòa nhà 2 m. Người ta muốn chế tạo một chiếc thang bắc từ mặt đất bên ngoài bức tường, gác qua bức tường và chạm vào tòa nhà (xem hình vẽ). Hỏi chiều dài tối thiểu của thang là bao nhiêu mét? (Kết quả làm tròn đến hàng phần trăm)

Trả lời: Chiều dài tối thiểu của thang là m.

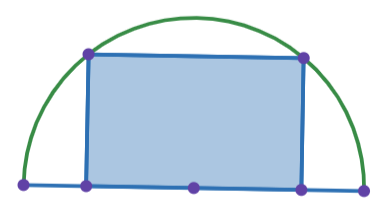
Từ một nửa hình tròn có bán kính 10 cm người ta cắt đi những phần thừa để có được hình chữ nhật (như hình vẽ). Hình chữ nhật này có diện tích lớn nhất bằng bao nhiêu?

Một cửa hàng bán 3 loại trái cây: táo, cam và quýt. Mỗi ngày, số lượng hộp quả táo, hộp quả cam và hộp quả quýt nhập về được ký hiệu lần lượt là x, y, z (x, y, z là các số tự nhiên). Cửa hàng có các thông tin và điều kiện như sau:

1) Chi phí nhập mỗi hộp quả táo là 100 000 đồng, mỗi hộp quả cam là 200 000 đồng và mỗi hộp quả quýt là 100 000 đồng.

2) Tổng chi phí nhập không được quá 1 000 000 đồng.

3) Cửa hàng phải nhập đủ cả 3 loại trái cây.

4) Cửa hàng cần ít nhất 3 hộp quả táo và cam cộng lại.

Lãi (lợi nhuận) thu về từ việc bán mỗi loại trái cây là: 200 000 đồng cho mỗi hộp quả táo, 300 000 đồng cho mỗi hộp quả cam và 100 000 đồng cho mỗi hộp quả quýt.

Giả định rằng tất cả số trái cây nhập về đều được bán hết trong ngày, hãy chỉ ra phương án nhập hàng giúp người bán hàng có được lợi nhuận cao nhất.

Đáp án: Phương án nhập 22.1 hộp quả táo, 22.2 hộp quả cam và 22.3 hộp quả quýt thì lợi nhuận của cửa hàng cao nhất.

Từ hình vuông có cạnh bằng 60 cm bạn Châu cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó bạn Châu gập thành hộp để đồ có dạng hình hộp chữ nhật không nắp. Tìm x để thể tích của khối hộp lớn nhất.

Trả lời: Vậy thể tích lớn nhất của hình hộp là V = 23.1 (cm³) khi x = 23.2 cm.

Một khách sạn có 50 phòng. Hiện tại mỗi phòng khách sạn cho thuê với giá 400 000 đồng một ngày và toàn bộ phòng đã được cho thuê hết. Biết cứ mỗi lần khách sạn tăng giá thuê phòng thêm 20 000 đồng mỗi ngày thì có thêm 2 phòng trống. Hỏi khách sạn nên tăng giá phòng thêm bao nhiêu để doanh thu trong một ngày của khách sạn là lớn nhất?

Trả lời: Khách sạn nên tăng giá phòng thêm nghìn đồng.

Một người chạy bộ ngược chiều gió trên một quãng đường có độ dài là s km, với vận tốc gió thổi là 6 km/h. Nếu vận tốc của người chạy khi không có gió là v (km/h) thì năng lượng tiêu hao của người đó trong t giờ được cho bởi công thức , trong đó c là một hằng số, E được tính bằng đơn vị Jun. Người đó cần chạy với vận tốc bao nhiêu km/h để năng lượng tiêu hao trong quá trình chạy là ít nhất?

Đáp án: Người đó cần chạy với vận tốc là km/h thì năng lượng tiêu hao trong quá trình chạy là ít nhất.

Nhà trường dự định dành ra một thửa đất có dạng hình chữ nhật trong mảnh đất lớn của trường để làm hồ cá sinh thái. Nhà trường dự định để phần đất ở giữa dạng hình chữ nhật để xây hồ cá, phần còn lại làm lối đi (như hình bên). Biết tổng diện tích thửa đất hình chữ nhật cần dùng là 864 m². Nhà trường nên chọn các kích thước của thửa đất hình chữ nhật là bao nhiêu để diện tích phần cho hồ cá là lớn nhất và tính giá trị lớn nhất đó.

Trả lời: Thửa đất hình chữ nhật đó nên có chiều dài là 26.1 m và chiều rộng là 26.2 m. Khi đó diện tích hồ cá có diện tích lớn nhất là 26.3 m².

Để chủ động nguồn nước ngọt cho sinh hoạt vào mùa hạn mặn, bác Minh thuê thợ xây một bể chứa nước hình hộp chữ nhật có nắp đậy với dung tích 9 m³ và có đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng. Nếu bác Minh muốn chi phí xây bể là thấp nhất có thể thì cần xây bể với kích thước như thế nào? Biết giá thuê thợ để xây bể là 550 000 đồng/m².

Đáp án: Cần xây bể có chiều rộng, chiều cao, chiều dài lần lượt là 27.1 m, 27.2 m, 27.3 m thì chi phí xây bể là thấp nhất.

Một sợi dây dài 200 cm được cắt thành hai đoạn. Đoạn dây thứ nhất được uốn thành hình tam giác đều, đoạn dây thứ hai được uốn thành hình lục giác đều. Hỏi tổng diện tích của hai hình này đạt giá trị nhỏ nhất khi cắt dây như thế nào?

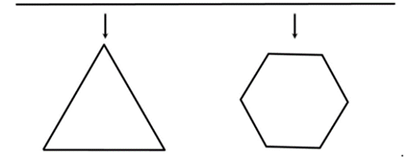
Trả lời: Sợi dây 200 cm cắt thành 2 đoạn có độ dài lần lượt là 28.1 cm và 28.2 cm. (Điền kết quả theo thứ tự giảm dần)