Đề thi thử môn Toán vào lớp 10 Sở Hà Nội năm 2026

Một cửa hàng bán các loại bánh truyền thống Việt Nam gồm: bánh chưng, bánh giầy, bánh khúc, bánh tẻ với các mức giá một chiếc lần lượt như sau: 55 000 đồng, 4 000 đồng, 13 000 đồng, 7 000 đồng.

Biểu đồ hình quạt tròn dưới đây biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) số lượng bánh bán được trong ngày 14/01/2023 của cửa hàng.

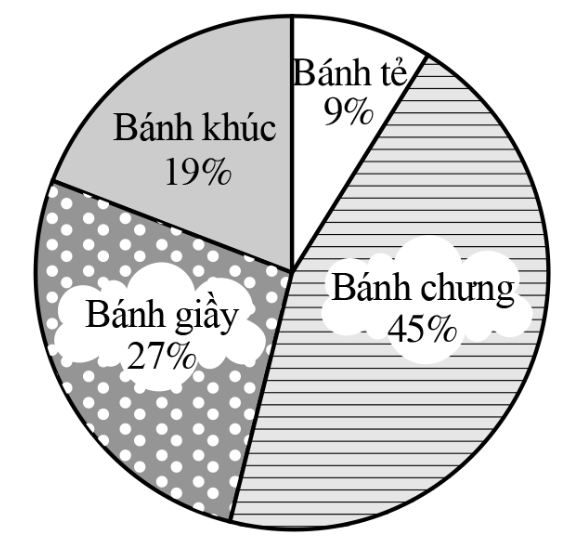
a) Loại bánh nào cửa hàng bán được nhiều nhất? Lí do phù hợp nhất để giải thích cho kết quả đó là gì?

b) Tính lượng tiền mà cửa hàng thu được từ bán bánh trong ngày 14/01/2023, biết tổng số các loại bánh cửa hàng bán trong ngày là 500 chiếc.

Đáp án: nghìn đồng.

Một hộp đựng 4 viên bi có cùng khối lượng và kích thước, được đánh số 5; 6; 7; 8. Lấy ngẫu nhiên lần lượt hai viên bi từ hộp đó (viên lấy ra lần đầu không trả lại vào hộp). Viết không gian mẫu của phép thử và tính xác suất của biến cố A: “Tổng hai số trên hai viên bi chia 3 dư 2”.

Trả lời:

Không gian mẫu của phép thử là:

{(5; 6); (5; 7); (3.1; 8); (6; 5); (6; 7); (6; 3.2); (7; 5); (7; 6); (7; 8); (8; 5); (8; 3.3); (8; 7)}

P(A) = 3.4. (Viết kết quả dưới dạng phân số tối giản a/b)

Cho hai biểu thức và với .

Tính giá trị của khi .

Đáp án: .

Rút gọn A ta được

Có bao nhiêu giá trị của để nhận giá trị nguyên?

Đáp án: Có giá trị của thỏa mãn.

Công ty địa ốc A xây một chung cư cao cấp có 100 căn hộ để bán gồm 2 loại: loại I là căn hộ 1 phòng ngủ giá bán 1,7 tỉ đồng /căn, loại II là căn hộ 2 phòng ngủ giá bán 2,6 tỉ đồng/căn. Do mục đích kinh doanh thay đổi nên có điều chỉnh giá bán như sau: tăng 10% đối với mỗi căn hộ loại I và giảm 5% đối với mỗi căn hộ loại II. Tổng số tiền bán hết các loại căn hộ là 211 tỉ đồng. Hỏi có bao nhiêu căn hộ loại I và loại II? 

Trả lời: Có 7.1 căn hộ loại I và 7.2 căn hộ loại II.

Cuối tuần Trang và Minh rủ nhau ra công viên tập thể dục. Cả hai cùng xuất phát từ một điểm bên bờ hồ có dạng hình tròn trong công viên, Trang đi xe đạp còn Minh chạy bộ phía sau. Trang hoàn thành một vòng quanh hồ trước Minh 24 phút và dừng lại ăn kem trong khi đợi Minh. Khi Minh đến chỗ đó, Trang đạp xe theo hướng ngược lại và Minh tiếp tục chạy bộ không dừng lại theo hướng cũ. Họ gặp nhau sau 5 phút. Giả sử tốc độ của cả hai không đổi, hỏi Minh mất bao lâu để hoàn thành một vòng quanh hồ?

Trả lời: Minh mất phút để hoàn thành một vòng quanh hồ.

Tìm để bất phương trình có nghiệm là .

Đáp án: 9.1; 9.2.

(Viết kết quả theo thứ tự tăng dần)

Từ một tấm bìa hình vuông cạnh 21 cm, bạn Nga cắt được một hình có dạng như hình vẽ (phần tô đậm và được bao quanh bởi đường liền nét). Biết rằng hình tròn diện tích và có tâm trùng với tâm của hình vuông. Các điểm là giao điểm của hai đường chéo hình vuông với đường tròn. Tính tổng độ dài đường viền của hình thu được (lấy và kết quả làm tròn đến hàng phần trăm).

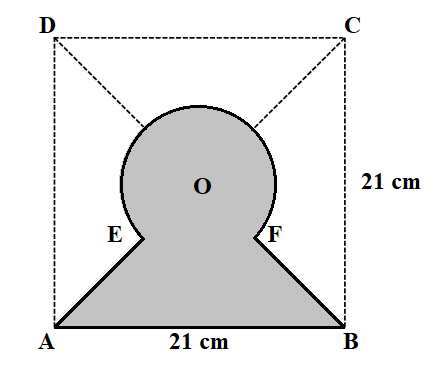
Đáp án: cm.

Cho đường tròn , đường kính vuông góc với dây tại điểm ( nằm giữa và ). Lấy điểm bất kì trên cung nhỏ ( khác và ). Gọi là giao điểm của và .

a) Chứng minh bốn điểm cùng thuộc một đường tròn.

Xét có: 11.1° (góc nội tiếp chắn nửa đường tròn) hay 11.2°

Xét vuông tại 11.3 có cạnh huyền , suy ra cùng thuộc đường tròn đường kính 11.4   (1)

Đường kính vuông góc với dây tại điểm nên  11.5°

Xét vuông tại 11.6 có cạnh huyền suy ra cùng thuộc đường tròn đường kính 11.7   (2)

Từ (1) và (2) suy ra bốn điểm cùng thuộc một đường tròn. (đpcm)

b) Gọi là giao điểm của tia và tia , là giao điểm của và . Chứng minh .

Xét có:

Suy ra là 12.1trọng tâmtrực tâmtâm đường tròn ngoại tiếp của

12.2 (tính chất đồng quy của ba đường cao)

Xét và , ta có:

là góc chung

12.3°

12.4 (g.g)

. (đpcm)

c) Kẻ vuông góc với tại . Gọi là trung điểm của , cắt tại . Chứng minh là tiếp tuyến của đường tròn ngoại tiếp tam giác và .

c.1) Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp tam giác PQE

- Theo ý b)

Xét vuông tại 13.1 có cạnh huyền , suy ra cùng thuộc đường tròn đường kính 13.2   (1)

Xét vuông tại 13.3 có cạnh huyền , suy ra cùng thuộc đường tròn đường kính 13.4  (2)

Từ (1) và (2) suy ra bốn điểm 13.5 cùng thuộc một đường tròn hay tứ giác nội tiếp đường tròn tâm 13.6, đường kính 13.7.

- Do tứ giác nội tiếp nên đường tròn ngoại tiếp tam giác chính là đường tròn ngoại tiếp tứ giác .

- Ta có:

Mà 13.8° nên 13.9° hay 13.10

Suy ra là tiếp tuyến của đường tròn ngoại tiếp tam giác . (đpcm)

c.2) Chứng minh KM // IF

+) Gọi là giao của và

Ta có 13.11 (hai bán kính của )

Và do có 13.12 nên là trung trực của 13.13

(13.14định lí Thales đảohệ quả của định lí Thalesđịnh lí Thales trong tam giác )

+) Xét và có:

13.15°

Góc 13.16 chung

13.17  (3)

+) Xét và có:

13.18°

là góc chung

13.19  (4)

Từ (3) và (4) suy ra

Mà 13.20 (13.21 là tâm đường tròn ngoại tiếp tứ giác )

Mà 13.22 nên

Từ (*) và (**) ta có

Suy ra (13.23định lí Thales đảohệ quả của định lí Thalesđịnh lí Thales). (đpcm)

Một công ty sản xuất hàng loạt thùng đựng hàng hóa bằng gỗ. Mỗi thùng có dạng hình hộp chữ nhật không nắp, đáy là hình vuông, thể tích 160 dm³. Để tiết kiệm vật liệu gỗ làm thùng, người ta cần thiết kế thùng sao cho tổng diện tích xung quanh và diện tích mặt đáy là nhỏ nhất. Khi đó độ dài cạnh đáy và chiều cao của thùng có giá trị bằng bao nhiêu? (Kết quả làm tròn đến một chữ số thập phân, chỉ làm tròn sau bước tính cuối cùng)

Trả lời: Thùng có cạnh đáy là 14.1 dm và chiều cao là 14.2 dm.