Đề thi chính thức vào 10 năm 2024 môn Toán - Sở GD&ĐT TPHCM (có giải thích đáp án chi tiết cho tài khoản FREE)

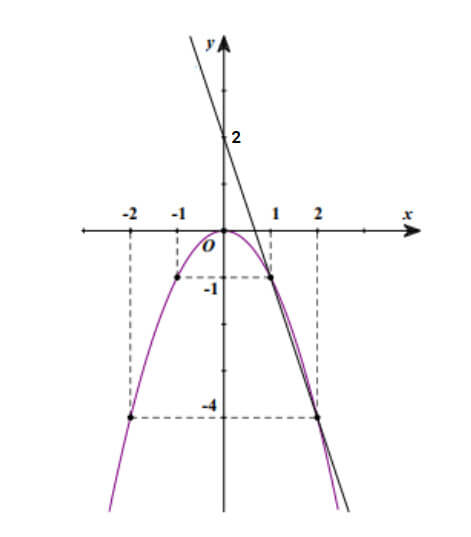
Cho parabol (P): y = -x² và đường thẳng (d): y = -3x + 2.

a) Đồ thị (P) và (d) trên cùng hệ trục tọa độ là:

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Đáp án: Tọa độ giao điểm hai hàm số (P) và (d) là C (2.1; 2.2), D (2.3; 2.4) (biết hoành độ điểm C nhỏ hơn hoành độ điểm D).

Cho phương trình có hai nghiệm là . Không giải phương trình hãy tính giá trị biểu thức (Viết đáp án dưới dạng phân số tối giản, ví dụ a/b).

Đáp án: A = .

Một khu vườn hình chữ nhật có chiều dài là 30m và chiều rộng là 20m. Bác Năm làm một lối đi cho khu vườn như hình vẽ (phần tô đậm).

a) Hãy viết biểu thức (thu gọn) theo x và y biểu thị phần diện tích còn lại của khu vườn.

Đáp án: Biểu thức biểu thị phần diện tích còn lại của khu vườn là:

S = 4.1 - 4.2y - 4.3x 

b) Tính diện tích phần còn lại của khu vườn khi x = 2,4m và y = 1,8m.

Đáp án: Diện tích phần còn lại của khu vườn là m².

Một cửa hàng xe máy điện cung cấp gói thuê pin theo tháng cho khách hàng dưới hai hình thức sau:

+) Gói linh hoạt, mức giá là 189 000 đồng/tháng, cho phép xe di chuyển tối đa 400 km. Nếu vượt số ki - lô - mét này, người dùng sẽ trả thêm 374 đồng cho mỗi ki-lô-mét vượt.

+) Gói cố định: mức giá là 350 000 đồng/tháng, không giới hạn số ki-lô-mét di chuyển.

Trung bình mỗi tháng anh Tâm di chuyển 800 km bằng xe máy điện. Hỏi anh Tâm nên thuê pin theo hình thức nào thì tiết kiệm hơn? Và tiết kiệm được bao nhiêu tiền mỗi tháng?

Đáp án: Anh Tâm nên sử dụng gói 6.1linh hoạtcố định thì tiết kiệm hơn và tiết kiệm được 6.2 đồng mỗi tháng.

Anh Huy là một nghệ nhân và anh đang thiết kế một mô hình Trái Đất dạng hình cầu có thể tích 4,2 dm³.

a) Tìm bán kính của mô hình Trái đất mà anh Huy thiết kế (kết quả làm tròn đến hàng đơn vị).

Đáp án: dm.

b) Anh Huy dự định làm một cái hộp bằng giấy (bao gồm cả nắp hộp) để dựng mô hình Trái đất (như hình vẽ trên). Anh đang phân vân nên làm hộp hình lập phương hay hộp hình trụ thì tốn ít giấy hơn. Hãy cho biết anh Huy nên chọn phương án nào? Biết các mặt hộp đều tiếp xúc với mô hình Trái đất và lượng giấy phát sinh là không đáng kể.

Cho biết công thức thể tích khối cầu là với R là bán kính khối cầu. Diện tích toàn phần hình trụ là với R là bán kính đáy hình trụ, h là chiều cao hình trụ.

Đáp án: Anh Huy nên làm hộp .

Lúc 7 giờ sáng, một xe máy xuất phát từ TP Hồ Chí Minh đi về hướng Biên Hòa với tốc độ trung bình 40 km/giờ. Sau đó 15 phút, một ô tô xuất phát từ Biên Hòa hướng Thành phố Hồ Chí Minh với tốc độ trunh bình 60 km/giờ. Hồ Chí Minh cách Biên Hòa 40 km.

- Gọi  là hàm số biểu diễn khoảng cách của xe máy so với TP Hồ Chí Minh sau khi đi được t giờ kể lúc 7 giờ 15 phút.

- Gọi  là hàm số biểu diễn khoảng cách của ô tô so với TP Hồ Chí Minh sau khi đi được t giờ kể từ lúc 7 giờ 15 phút.

a) Tìm các hệ số a, b, c, d.

Đáp án: a = 9.1, b = 9.2, c = 9.3, d = 9.4.

b) Hỏi hai xe gặp nhau lúc mấy giờ và nơi gặp nhau cách Thành phố Hồ Chí Minh bao nhiêu ki-lô-mét?

Đáp án: Hai xe gặp nhau lúc 10.1 giờ 10.2 phút, cách Thành phố Hồ Chí Minh 10.3 km.

Hai thùng chứa nước hình trụ đều được gắn một vòi chảy ở đáy thùng. ban đầu chiều cao mực nước ở thùng thứ nhất hơn thùng thứ hai 0,2m , để vệ sinh hai thùng này bạn Hân cần mở vòi cho nước chảy hết ra ngoài. Bạn Hân bắt đầu mở vòi cho thùng thứ nhất chảy từ 8 giờ sáng và sau đó 3 phút bắt đầu mở vòi cho thùng thứ hai chảy. Khi quan sát quá trình chảy của hai thùng, Hân thấy rằng:

 - Tại thời điểm 8 giờ 04 phút thì chiều cao mực nước hai thùng bằng nhau.

- Tại thời điểm 8 giờ 08 phút thì thùng thứ hai vừa chảy hết nước và chiều cao mực nước còn lại ở thùng thứ nhất là 0,4m.

Tìm chiều cao mực nước ban đầu ở mỗi thùng. Biết rằng tốc độ chảy ở mỗi vòi là không đổi.

Đáp án: Chiều cao mực nước ban đầu ở thùng thứ nhất, thùng thứ hai lần lượt là 11.1m, 11.2m.

Từ điểm A nằm bên ngoài đường tròn (O; R), kẻ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm), AO cắt BC tại K.

a) Điền vào chỗ trống để hoàn thiện phép chứng minh ABOC là tứ giác nội tiếp và AO là đường trung trực của đoạn thẳng BC.

1, Do AB, AC là tiếp tuyến nên 12.1

Xét tứ giác OBAC có: 12.2 + 12.3 = 12.4

Mà 2 góc này ở vị trí đối diện nên tứ giác OBAC nội tiếp (dhnb)

2, Ta có: AB = AC (tính chất hai tiếp tuyến cắt nhau) nên điểm 12.5 nằm trên đường trung trực của BC. (1)

Ta có: OB = OC = R nên điểm 12.6 nằm trên đường trung trực của BC (2)

Từ (1) và (2) suy ra OA là trung trực của 12.7 (đpcm)

b) Gọi P là điểm bất kì thuộc (O) sao cho tia BO nằm giữa hai tia BP và BC, H là chân đường vuông góc kẻ từ B xuống PC, M là trung điểm BH và PM cắt (O) tại Q (khác P). Điền vào chỗ trống để hoàn thiện phép chứng minh .

1, Do M là trung điểm của BH (gt), K là trung điểm của BC (cmt)

Nên 13.1 là đường trung bình của tam giác BHC

13.2 // PC (2 góc đồng vị)

2, Mà (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung 13.3

(đpcm).

c) Điền vào chỗ trống để hoàn thiện phép chứng minh và .

1,Từ câu b) (cùng chắn cung 14.1) nên tứ giác BMKQ nội tiếp

14.2

Do MK // HC  14.3 nên 14.4 hay 14.5 (3)

2,  nên  14.6   14.7 (4)

Từ (3), (4) , mà (cùng chắn cung 14.8)

hay tứ giác QKCA nội tiếp

(đpcm)

3, Gọi L là giao điểm còn lại của AQ với (O)

Vì 14.9 - 14.10 nên hiển nhiên C, O, L thẳng hàng, hay CL = 14.11R

4, Ta có: (cùng chắn cung 14.12)

Vậy (đpcm).