Đề thi chính thức vào 10 môn Toán Sở Bạc Liêu năm 2020
2/5/2025 9:05:00 AMRút gọn biểu thức .
Tìm điều kiện của x để biểu thức có nghĩa.
Giải hệ phương trình .
Đáp án: Hệ phương trình có nghiệm x = , y = . (Viết đáp án dưới dạng phân số a/b hoặc -a/b).
Cho parabol (P): y = 2x2 và đường thẳng (d): y = 3x +b . Xác định giá trị của b để đường thẳng (d) tiếp xúc với parabol (P).
Đáp án: b = (Viết đáp án dưới dạng phân số tối giản. VD: 1/2 hoặc -1/2).
Cho phương trình: (1) (với m là tham số)
a) Giải phương trình (1) khi m = 4.
- S = {1; 4}
- S = {-1; 4}
- S = {-1;- 4}
- S = {1; -4}
b) Tìm m để phương trình (1) có nghiệm.
c) Xác định các giá trị của m để phương trình (1) có hai nghiệm phân biệt x1, x2 thỏa mãn x1(3 + x1) + x2(3 + x2) = - 4.
Đáp án: m = .
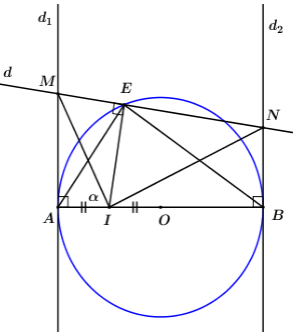
Cho đường tròn tâm O đường kính AB = 2R. Gọi I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn (O) sao cho E không trùng với A và B. Dựng đường thẳng d1 và d2 lần lượt là các tiếp tuyến của đường tròn (O) tại A và B. Gọi d là đường thẳng qua E và vuông góc với EI. Đường thẳng d cắt d1, d2 lần lượt tại M, N.
a) Điền vào chỗ trống để hoàn thành phép chứng minh tứ giác AMEI nội tiếp.
1. Vì d1 là tiếp tuyến của (O) tại A nên =
2. Vì d ⊥ EI tại E nên =
3. Xét tứ giác AMEI có:
=
+
=
Vậy tứ giác AMEI là tứ giác nội tiếp.
b) Điền vào chỗ trống để hoàn thành phép chứng minh ∆IAE đồng dạng với ∆NBE. Từ đó chứng minh IB. NE = 3IE. NB.

1. Vì là góc nội tiếp chắn nửa đường tròn nên
=
Ta có: =
=
(do
)
(cùng phụ với
).
2. Xét ∆IAE và ∆NBE có:
(cmt);
(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung )
(hai cạnh tương ứng)
(1).
3. Mà I là trung điểm của OA (gt)
Lại có O là trung điểm của AB = IA
.
4. Khi đó ta có:
(1) (nhân cả 2 vế với 3)
(đpcm).
c) Điền vào chỗ trống để hoàn thành phép chứng minh ∆MNI vuông tại I .

1. Xét tứ giác BNEI có:
=
(do
tại E)
=
(do d2 là tiếp tuyến của đường tròn (O) tại )
=
+
=
Tứ giác BNEI là tứ giác nội tiếp
(hai góc nội tiếp cùng chắn cung ).
2. Lại có: Tứ giác AMEI là tứ giác nội tiếp (ý a)
(hai góc nội tiếp cùng chắn cung ).
3. Xét tam giác MNI có:
=
(do
(cmt) nên ∆AEB vuông tại E)
∆MNI vuông tại I.
d) Tìm giá trị nhỏ nhất của SMNI theo R.