Đề thi chính thức vào 10 năm 2020 môn Toán - Sở GD&ĐT Bến Tre

7/5/2022 2:32:00 PM

Trục căn thức ở mẫu của biểu thức .

Tìm x biết .

Đáp án: x = .

Cho hàm số bậc nhất: .

Hàm số trên đồng biến hay nghịch biến trên ? Vì sao ?

Đáp án: Hàm số trên trên .

Tính giá trị của y khi .

Đáp án: y = .

Cho hàm số: y = 2x2 có đồ thị (P).

a) Đồ thị hàm số (P): y = 2x2 trên mặt phẳng Oxy là:

b) Tìm tọa độ các điểm thuộc (P) có tung độ bằng 2.

  • (1; 2), (-1; 2)

  • (1; -2), (-1; 2)

  • (-1; - 2), (-1; 2)
  • (1; 2)

Giải phương trình: .

Giải hệ phương trình:.

Đáp án: x = ; y = .

Tìm các giá trị của tham số m để phương trình: có hai nghiệm phân biệt.

Với giá trị nào của tham số m thì đồ thị của hàm số y = x + (5 +m) và y = 2x + (7 - m) cắt nhau tại một điểm nằm trên trục hoành? 

Đáp án: m = .

Cho tam giác ABC vuông tại B có đường cao BH , biết AB = 6 cm, AC = 10 cm. Tính độ dài các đoạn thẳng BC, BH.

Đáp án: BC = cm, BH = cm. (Viết đáp án dưới dạng số thập phân a,b)

Trên đường tròn (O) lấy hai điểm A, B sao cho và điểm C như hình vẽ. Tính số đo cung AmB, số đo cung ACB và số đo góc ACB.

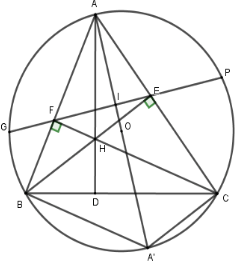
Cho tam giác nhọn ABC nội tiếp đường tròn (O) và có các đường cao BE, CF cắt nhau tại H (E ∈ AC, F ∈ AB).

a) Điền vào chỗ trống để hoàn thành phép chứng minh tứ giác AEHF nội tiếp.

1. Ta có:

2. Tứ giác AFHE có + =

⇒ Tứ giác AFHE nội tiếp.

b) Điền vào chỗ trống để hoàn thành phép chứng minh AH ⊥ BC.

 1. Kéo dài AH cắt BC tại D.

2. Do BE, CF là các đường cao trong tam giác và BE ∩ CF = {H} nên là trực tâm của ∆ABC

⇒ AD là đường cao trong ∆ABC ⇒ AD ⊥ ⇒ AH ⊥ BC (đpcm).

c) Gọi P, G là hai giao điểm của đường thẳng EF và đường tròn (O) sao cho điểm E nằm giữa điểm P và điểm F.  Điền vào chỗ trống để hoàn thành phép chứng minh AO là đường trung trực của đoạn thẳng PG.

1. Xét tứ giác BFEC có = nên là tứ giác nội tiếp

(cùng bù với ) (1)

2. Kẻ đường kính AA'. Gọi I là giao điểm của AO và PG.

3. Tứ giác BACA' nội tiếp nên (cùng chắn cung ) (2)

Từ (1) và (2) suy ra:

Mà  (góc nội tiếp chắn nửa đường tròn)

Nên hay

⇒ AO ⊥ PG tại (3).

4. Do đó: là trung điểm của PG (tính chất đường kính dây cung) (4)

5. Từ (3) và (4) suy ra: AO là đường trung trực của PG.