Hình chữ nhật

3/2/2023 9:25:00 AM

Điền cụm từ thích hợp vào chỗ chấm.

Hình bình hành có .... bằng nhau là hình chữ nhật.

hai cạnh đối
hai góc đối
hai đường chéo
hai cạnh kề

Điền cụm từ thích hợp vào chỗ chấm

Nếu tam giác có một đường trung tuyến bằng nửa cạnh tương ứng thì ...

tam giác đó là tam giác cân.
tam giác đó là tam giác đều.
tam giác đó là tam giác vuông.
tam giác đó là tam giác tù.

Một dấu hiệu nhận biết của hình chữ nhật là:

Tứ giác có hai đường chéo bằng nhau.
Hình thang có hai góc vuông là hình chữ nhật.
Hình bình hành có một góc vuông là hình chữ nhật.
Hình bình hành có hai đường chéo vuông góc là hình chữ nhật.

Tính diện tích của hình chữ nhật ABCD, biết AB = 6cm và BC = 8cm.

Đáp án: Diện tích của hình chữ nhật ABCD là: cm².

Cho hình thang cân ABCD (AB // CD) có hai đường cao AH và BK.

Điền vào ô trống để hoàn thành phép chứng minh tứ giác ABKH là hình chữ nhật.

Chứng minh

Ta có: , suy ra AH // 5.1

Xét tứ giác ABKH có:

AB // HK (gt) và AH // 5.2

Suy ra tứ giác ABKH là hình bình hành (các cặp cạnh đối song song)

Mà 5.3^o

Suy ra tứ giác ABKH là hình chữ nhật (hình bình hành có 1 góc vuông) (đpcm).

Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Trên tia đối của tia IH lấy điểm D sao cho IH = ID.

Điền vào ô trống để hoàn thành phép chứng minh tứ giác AHCD là hình chữ nhật.

Chứng minh

Xét tứ giác AHCD có:

AC giao HD tại 6.1

IH = ID (gt)

IA = 6.2 (I là trung điểm AC)

Suy ra tứ giác AHCD là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường)

Mà góc 6.3 = 90^o

Suy ra tứ giác AHCD là hình chữ nhật (hình bình hành có 1 góc vuông) (đpcm).

Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M thuộc AB).

Điền vào ô trống để hoàn thành phép chứng minh tứ giác PCQM là hình chữ nhật.

Chứng minh

1) Ta có:

+) vuông cân tại C nên (1)

+) PM // BC suy ra (hai góc đồng vị) (2)

Từ (1) và (2) suy ra

Suy ra vuông cân tại 7.1

Suy ra AP = PM

Mà AP = CQ (gt) suy ra PM = CQ

2) Xét tứ giác PCQM có

PM // CQ (do PM // BC)

PM = CQ (cmt)

Suy ra tứ giác PCQM là hình bình hành (cặp cạnh đối song song và bằng nhau)

Mà = 7.2^o

Suy ra tứ giác PCQM là hình chữ nhật (hình bình hành có 1 góc vuông) (đpcm).

Cho tam giác ABC có M là trung điểm AC. Biết AM = BM, khi đó tam giác ABC là

Tam giác cân
Tam giác đều
Tam giác vuông
Tam giác nhọn

Cho tam giác ABC vuông tại A, từ điểm D trên cạnh BC (D khác B, C) vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Điền vào ô trống để hoàn thành phép chứng minh tứ giác AEDF là hình chữ nhật.

Chứng minh

Ta có:

tại E nên 9.1^o

tại F nên 9.2^o

Xét tứ giác AEDF có:

9.3^o

Suy ra tứ giác AEDF là hình chữ nhật (tứ giác có 3 góc vuông) (đpcm).

Gọi I là trung điểm của EF.

Điền vào ô trống để hoàn thành phép chứng minh ba điểm A, I, D thẳng hàng.

Tứ giác AEDF là hình chữ nhật nên

EF và 10.1 cắt nhau tại trung điểm mỗi đường

Mà I là trung điểm của EF

Suy ra I cũng là trung điểm của 10.2

Suy ra ba điểm A, I, D thẳng hàng (đpcm).

Tính diện tích của hình chữ nhật ABCD, biết AD = 7cm và CD = 12cm.

Đáp án: Diện tích của hình chữ nhật ABCD là: .

Cho tam giác ABC vuông ở A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc kẻ từ H đến AB, AC.

Điền vào chỗ trống để hoàn thành phép chứng minh tứ giác EAFH là hình chữ nhật.

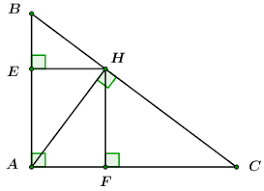
Tứ giác EAFH có:

Suy ra: EAFH là hình chữ nhật (vì có 3 góc vuông).

Qua A kẻ đường vuông góc với EF, cắt BC ở I.

Điền vào chỗ trống để hoàn thành phép chứng minh I là trung điểm của BC.

Trong tam giác AHB có mà

Suy ra (1)

Gọi O là giao điểm hai đường chéo EF và 13.1 của hình chữ nhật AEHF thì OA = OF

Do đó cân tại 13.2 nên (2)

Từ (1) và (2) suy ra

Mặt khác ta lại có:

và

Suy ra

Do đó: cân tại 13.3 nên IA = IC

Chứng minh tương tự ta được: IB = IA

Suy ra: IB = IC.

Vậy I là trung điểm của BC (đpcm).

Cho tam giác ABC vuông tại A, đường cao AD. Gọi M là một điểm bất kì trên cạch BC. Vẽ .

Điền vào chỗ trống để hoàn thành phép chứng minh tam giác DEF vuông cân.

1) Tứ giác AEMF có

Suy ra tứ giác AEMF là hình chữ nhật (tứ giác có 3 góc vuông)

AE = 14.1 (1)

2) vuông cân tại A nên

vuông tại F có nên vuông cân tại F

CF = 14.2 (2)

Từ (1) và (2) suy ra AE = CF

3) vuông cân tại A có AD là đường cao nên AD đồng thời là đường trung tuyến, đường phân giác của

Từ đó ta có: AD = DC = 14.3 BC;

(Viết dưới dạng phân số tối giản. VD: 1/2 hoặc -1/2)

Xét và ta có:

AE = CF (cmt)

AD = 14.4 (cmt)

(cmt)

Suy ra:

14.5 = DF và (cạnh và góc tương ứng)

4) Ta có:

Xét có DE = DF và

Suy ra là tam giác vuông cân tại D (đpcm).

Hãy chọn đáp án đúng. Hình bình hành ABCD là hình chữ nhật khi:

Cho tam giác ABC, đường cao AH. I là trung điểm của AC, E đối xứng với H qua I. Tứ giác AHCE là hình gì?

Hình thang cân
Hình thang
Hình chữ nhật
Hình thang vuông

Hình chữ nhật ABCD có O là giao điểm của hai đường chéo. Biết , tính số đo .

Trả lời: Số đo là

Cho tam giác ABC vuông cân tại A, AC = 6 cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Tính chu vi tứ giác ADME.

Trả lời: Chu vi tứ giác là cm.