Định lí Thalès trong tam giác
2/12/2023 9:40:00 AMCho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Xét các khẳng định sau:
Số khẳng định đúng trong các khẳng định trên là:
- 1
- 2
- 0
- 3
Tìm độ dài của x trong hình bên, biết MN // BC.
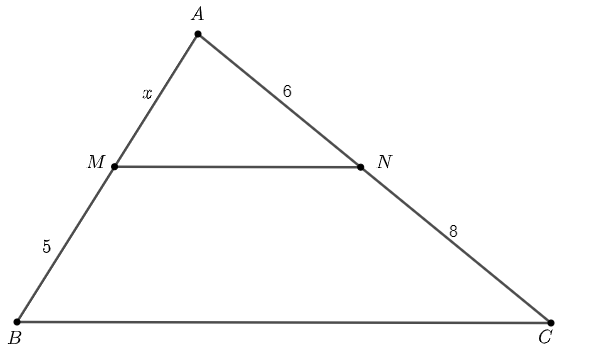
Đáp án: x = . (Học sinh viết đáp án dưới dạng số thập phân)
Cho tam giác ABC cân tại A có AB = 10 cm. Lấy điểm M trên đoạn AB sao cho AM = 4 cm, qua M kẻ đường thẳng d song song với BC cắt AC tại N. Tính độ dài AN.
- 4 cm
- 6 cm
- 8 cm
- 10 cm
Cho góc xOy. Trên tia Ox, lấy theo thứ tự 2 điểm A, B sao cho OA = 2 cm, AB = 3 cm. Trên Oy, lấy điểm C với OC = 3 cm. Từ B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài CD.
Đáp án: CD = cm. (Học sinh viết đáp án dưới dạng số thập phân)
Quan sát hình dưới đây và tìm giá trị của x.
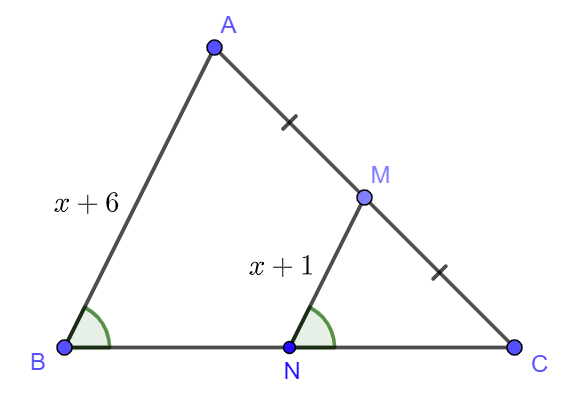
Đáp án: x = .
Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự tại D và E. Qua E kẻ đường thẳng song song với CD, cắt AB tại F. Biết AB = 16 cm, AF = 9 cm. Tính độ dài của AD.
Đáp án: AD = cm.
Cho tam giác ABC, đường trung tuyến AD. Gọi K là điểm thuộc đoạn thẳng AD sao cho . Gọi E là giao điểm của BK và AC. Tính tỉ số
.
Đáp án: = . (Học sinh viết đáp án dưới dạng phân số tối giản a/b)
Cho hình thang ABCD (AB // CD). Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự tại E, F. Khẳng định đúng trong các khẳng định dưới đây là:
Cho hình bình hành ABCD có M, N lần lượt là trung điểm của AB và CD. Gọi P, Q lần lượt là giao điểm của AN và CM với đường chéo BD. Tính độ dài đoạn thẳng BQ, biết DP = 3 cm.
Đáp án: BQ = cm.
Cho hình thang ABCD (AB // CD) có diện tích 36 cm2, AB = 4 cm, CD = 8 cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
Đáp án: Diện tích tam giác COD là cm2.