Hai tam giác đồng dạng
3/19/2023 9:40:00 AMCho ΔMNP ᔕ ΔABC có MN = 4 cm; AB = 6 cm. Khi đó ΔMNP ᔕ ΔABC với tỉ số k bằng:
Cho ΔABC ᔕ ΔMNP. Nếu tam giác ABC cân tại đỉnh B thì:
ΔMNP cân tại đỉnh M
ΔMNP cân tại đỉnh N
ΔMNP cân tại đỉnh P
ΔMNP đều
Cho góc xOy. Trên tia Ox, lấy theo thứ tự 2 điểm A, B sao cho OA = 2 cm, AB = 3 cm. Trên Oy, lấy điểm C với OC = 3 cm. Từ B kẻ đường thẳng song song với AC cắt Oy tại D.
Điền vào ô trống để hoàn thành phép chứng minh ΔOAC ᔕ ΔOBD.
Chứng minh
Xét ΔOBD có CA // ( ∈ OD; ∈ OB)
Suy ra ΔOAC ᔕ ΔOBD (đpcm).
ΔOAC ᔕ ΔOBD đồng dạng với tỉ số k. Tìm k.
Đáp án: k = (Viết đáp án dưới dạng phân số tối giản a/b)
Tính độ dài CD.
Đáp án: CD = cm. (Viết đáp án dưới dạng phân số tối giản a/b)
Cho biết
. Tính số đo của góc F.
Đáp án:
.
Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.
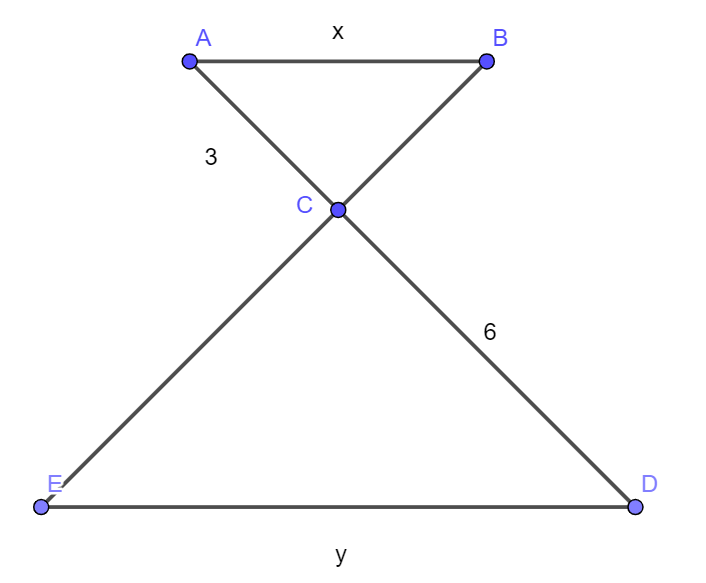
Đáp án: Tỉ số = . (Viết đáp án dưới dạng phân số tối giản a/b)
Cho . Biết AB = 5 cm, BC = 6 cm, MN = 10 cm, MP = 5 cm. Khẳng định nào dưới đây là đúng?
- NP = 2,5 cm và AC = 12 cm.
- NP = 12 cm và AC = 2,5 cm.
- NP = 5 cm và AC = 10 cm.
- NP = 10 cm và AC = 5 cm.
Cho biết AB = 18 cm, AC = 24 cm, BC = 30 cm, MN = 6 cm, MP = 8 cm, NP = 10 cm và
. Khẳng định nào dưới đây là đúng?
Cho theo tỉ số
, biết
có chu vi bằng 42 cm. Tính chu vi của
.
Đáp án: Chu vi của là cm.