Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 (Cánh diều)

Kết quả của phép tính bằng

Trong mặt tọa độ Oxy cho hai đường Parabol như hình vẽ.

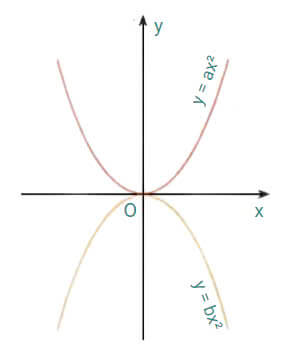
Khẳng định nào sau đây là đúng?

Tìm điều kiện xác định của phương trình:

Hai số u = m; v = 1 - m là nghiệm của phương trình nào dưới đây?

Cho hệ phương trình , với m là tham số. Trong những nhận định sau, những nhận định nào đúng về nghiệm của hệ phương trình đã cho?

(I) Hệ phương trình có nghiệm duy nhất với mọi m.

(II) Hệ phương trình có vô số nghiệm khi m = -1.

(III) Hệ phương trình vô nghiệm khi m = 1.

(IV) Hệ phương trình có nghiệm duy nhất khi .

Một chiếc mũ sinh nhật dạng hình nón được làm bằng giấy, có chu vi đáy là 62,8 cm và đường sinh có độ dài 30 cm. Giả sử diện tích phần mép nối không đáng kể. Diện tích giấy để làm nên chiếc mũ đó là

Cho hình vẽ, biết AC là đường kính của (O) và góc BDC bằng 60^o.

Số đo góc x bằng 

Vẽ trên giấy 18 hình tam giác đều bằng nhau và có vị trí như hình dưới (còn gọi là hình chong chóng). Biết hình chong chóng có 6 điểm mút sao cho 6 điểm này là các đỉnh của một hình lục giác đều tâm O.

Cho phép quay thuận chiều α với tâm O giữ nguyên các đỉnh của hình lục giác đều, tìm α biết 120^o < α < 200^o.

Cho vuông tại M. Biết . Giá trị của  bằng:

Cho đường tròn và hai điểm . Biết rằng và . Khi đó:

Một gia đình có nuôi 20 con mèo, người chủ thống kê số tuổi của những con mèo và thu được bảng sau:

Hỏi gia đình người chủ có bao nhiêu con mèo từ 4 tuổi trở lên?

Một hộp đựng 5 quả cầu màu xanh, 3 quả cầu màu đỏ, 7 quả cầu màu trắng có cùng kích thước và khối lượng. Chọn ngẫu nhiên ra một quả cầu. Xác suất của biến cố “Quả cầu được chọn ra không có màu đỏ” là

Cho phương trình (với m là tham số). Các khẳng định sau đúng hay sai?

a) Khi m = 1 thì phương trình có 2 nghiệm .

b) Phương trình (1) có 2 nghiệm thỏa mãn .

c) Phương trình (1) có 2 nghiệm  thỏa mãn  .

d) Phương trình (1) có hai nghiệm phân biệt thỏa mãn điều kiện khi m = 3.

Trong năm học 2024 - 2025, trường Trung học cơ sở X tổ chức cho học sinh khối 9 đăng ký tham gia đội tuyển Toán và đội tuyển Khoa học tự nhiên cấp trường. Ở học kỳ I, số lượng học sinh tham gia đội tuyển Toán ít hơn số lượng học sinh tham gia đội tuyển Khoa học tự nhiên là 50 em. Sang học kỳ II, có 5 em chuyển từ đội tuyển Khoa học tự nhiên sang đội tuyển Toán nên số lượng học sinh của đội tuyển Toán bằng số lượng học sinh đội tuyển Khoa học tự nhiên. Biết rằng trong năm học, tổng số học sinh tham gia cả hai đội tuyển không thay đổi và mỗi học sinh chỉ tham gia một đội tuyển. Gọi x (học sinh) là số lượng học sinh tham gia đội tuyển Toán ở học kì I (x ∈ ℕ*). Các khẳng định sau đúng hay sai?

a) Số lượng học sinh tham gia đội tuyển Khoa học tự nhiên ở học kì I là  (học sinh). 

b)

c) Có 105 học sinh tham gia đội tuyển Toán và 155 học sinh tham gia đội tuyển Khoa học tự nhiên ở học kì I.

d) Tổng số học sinh tham gia cả hai đội tuyển là 280 em.

Bác Tú cần làm 10 khối bê tông hình trụ bao quanh ở các gốc cây trong vườn. Biết đáy của khối bê tông là hình vành khăn có bề rộng là 9 cm, chiều cao 10 cm và đường kính đáy của hình trụ lớn là 90 cm (như hình vẽ) (π = 3,14). Các khẳng định sau đúng hay sai?

a) Bán kính đáy hình trụ nhỏ bên trong khối bê tông là 36 cm.

b) Thể tích hình trụ nhỏ bên trong khối bê tông là 40 694,4 cm³.

c) Thể tích của một khối bê tông là 63 580 cm³.

d) Tiền công đổ 1 m³ bê tông là 1 triệu 150 nghìn đồng. Số tiền công bác Tú cần trả để làm 10 khối bê tông như trên khoảng 360 nghìn đồng.

Khảo sát các học sinh lớp 6 của một số trường Trung học cơ sở trên địa bàn thành phố X về thời gian sử dụng mạng xã hội trung bình trong một ngày (đơn vị: giờ), kết quả thu được như hình bên dưới. Biết rằng có 66 bạn sử dụng mạng xã hội từ 4,5 giờ trở lên. Các khẳng định sau đúng hay sai?

a) Có 200 học sinh tham gia cuộc khảo sát.

b) Có 1 743 học sinh có thời gian sử dụng mạng xã hội trung bình trong một ngày dưới 3 giờ.

c) Một người cho rằng có trên 50% học sinh tham gia khảo sát sử dụng mạng xã hội từ 3 giờ trở lên mỗi ngày.

d) Chọn ngẫu nhiên một học sinh đã tham gia khảo sát. Xác suất chọn được học sinh sử dụng mạng xã hội ít nhất 1,5 giờ mỗi ngày là 0,533.

Cho hệ phương trình , với m là tham số. Tìm giá trị nguyên nhỏ nhất của m để hệ phương trình có nghiệm (x; y) thỏa mãn .

Trả lời: m = . 

Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8 000 quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ. Tìm số máy móc công ty nên sử dụng để chi phí sản xuất 8 000 quả bóng là thấp nhất.

Trả lời: Công ty nên sử dụng máy để chi phí sản xuất là thấp nhất.

Cho biểu thức: với . Tìm x để A đạt giá trị nhỏ nhất.

Trả lời: x = . (Kết quả viết dưới dạng phân số tối giản a/b)

Cho tứ giác ABCD nội tiếp đường tròn (O) có hai tia BA, CD kéo dài cắt nhau tại M sao cho và hai tia DA, CB kéo dài cắt nhau tại N sao cho . Tính số đo của .

Trả lời: = °.

Một con đê được đắp chắn sóng theo hình dưới (BC // AD, H và K lần lượt là hình chiếu của B và C trên AD), độ dài dốc của con đê phía sông là 7 m. Hỏi độ dài dốc ở phía còn lại của con đê dài bao nhiêu mét? (Kết quả làm tròn đến chữ số thập phân thứ hai; chỉ làm tròn sau bước tính cuối cùng)

Trả lời: Độ dài dốc ở phía còn lại của con đê gần bằng m.

 Một túi có 2 viên bi đỏ và 3 viên bi xanh, các viên bi có cùng kích thước và khối lượng. Bốc ngẫu nhiên lần lượt hai viên bi, viên bi bốc ra lần đầu không hoàn lại. Tính xác suất để cả hai viên bi được bốc ra cùng màu.

Trả lời: Xác suất để cả hai viên bi được bốc ra cùng màu là . (Viết kết quả dưới dạng phân số tối giản a/b)