Vị trí tương đối của đường thẳng và đường tròn
6/1/2024 5:40:09 PMCho (O; 5 cm), gọi d là khoảng cách từ O tới đường thẳng a.
Xác định số điểm chung giữa đường thẳng a và (O), biết d = 7 cm.
- 3 điểm chung
- 2 điểm chung
- 1 điểm chung
- 0 điểm chung
Với thì số giao điểm của đường thẳng a với (O) là .
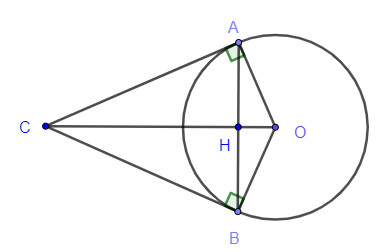
Cho (O; 5 cm) và điểm C sao cho CO bằng 10 cm. Từ C kẻ tiếp tuyến CA, CB với (O) (A, B là các tiếp điểm). Gọi H là giao điểm của CO và AB.
Trong các khẳng định sau, khẳng định nào đúng?
Tính số đo góc ACB.
Đáp án: o

Độ dài cạnh AC bằng

Độ dài cạnh AB là
Trong mặt phẳng tọa độ Oxy, cho điểm A(-2; 3). Hãy xác định vị trí tương đối của đường tròn (A; 3) với các trục tọa độ.
- Trục hoành không cắt đường tròn và trục tung tiếp xúc với đường tròn.
- Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
- Cả hai trục tọa độ đều cắt đường tròn
- Cả hai trục tọa độ đều tiếp xúc với đường tròn.
Bạn Mai cắt 4 hình tròn bằng giấy có bán kính lần lượt là 5 cm, 8 cm, 9 cm và 12 cm để dán trang trí lên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 9 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 9 cm). Bạn Mai dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b. Hãy cho biết trị trí tương đối của đường thẳng a với các hình tròn đã cho.
Kết luận: Đường thẳng a hình tròn có bán kính 5 cm.
Đường thẳng a hình tròn có bán kính 8 cm.
Đường thẳng a hình tròn có bán kính 9 cm.
Đường thẳng a hình tròn có bán kính 12 cm.
Cho đường tròn (O; 15 cm) có dây AB = 24 cm. Một tiếp tuyến của (O) song song với AB và lần lượt cắt tia OA, OB tại E và F.
Độ dài đoạn thẳng EF là
Cho hình thang vuông ABCD (góc A và D bằng 90o) có O là trung điểm của AD và góc BOC bằng 90o.
Điền vào ô trống để hoàn thành phép chứng minh BC là tiếp tuyến của đường tròn đường kính AD.
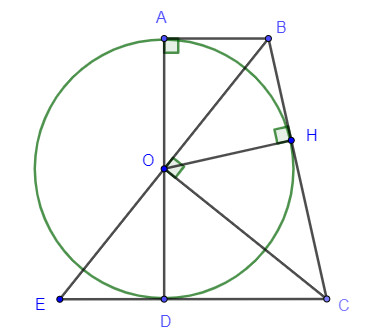
Kéo dài BO cắt DC tại E.
Do góc BOC bằng 90o nên góc COE bằng 90o vì 2 góc này là hai góc kề bù.
Ta có AB // ED nên theo định lí Thales ta có:
Suy ra BO = nên CO là đường trung tuyến của tam giác CBE.
Xét tam giác ECB có CO là đường cao đồng thời là đường trung tuyến nên tam giác ECB cân tại C, khi đó:
Kẻ OH vuông góc với BC tại H.
Xét tam giác OED và tam giác OHB có:
BO =
o
Suy ra △ OED = △ ()
Suy ra OD = (2 cạnh tương ứng)
Mà OD = OA = R nên OD = OA = OH = R hay A, H, D cùng thuộc (O)
Ta có:
Suy ra BC là tiếp tuyến của (O)
Vậy BC là tiếp tuyến của đường tròn đường kính AD.