Đề thi khảo sát chất lượng đầu năm môn Toán lớp 8 (Cánh diều)

6/24/2025 3:38:00 PM

Cho tam giác ABC có đường trung tuyến AD = 15 cm (D ∈ BC). Gọi G là trọng tâm của tam giác ABC, khi đó độ dài DG bằng:

10 cm
4 cm
6 cm
5 cm

Cho đa thức . Giá trị của là:

Một hộp có 15 chiếc thẻ cùng loại, được đánh các số từ 1 đến 15. Rút ngẫu nhiên một chiếc thẻ trong hộp. Xác suất của biến cố "Số xuất hiện trên thẻ được rút ra là số tròn chục" là:

Giá trị của x thỏa mãn tỉ lệ thức là:

Đa thức có hệ số cao nhất là:

-3
5
-2
10

Mỗi quyển sách giá x đồng, mỗi chiếc bút giá y đồng. Lan tới hiệu sách mua 6 chiếc bút và 10 quyển sách, số tiền Lan phải trả được tính bởi công thức nào dưới đây?

10x - 6y
10x + 6y
6x + 10y
6x - 10y

Cho x tỉ lệ nghịch với y theo hệ số tỉ lệ là -2. Khi y = -5 thì giá trị của x là:

Một hộp bi có chứa 12 bi đỏ, 10 bi xanh, 8 bi vàng. Biến cố nào dưới đây là biến cố không thể?

Lấy được 2 viên bi cùng màu.
Lấy được 3 viên bi có đủ cả 3 màu đỏ, xanh, vàng.
Lấy được 1 viên bi có màu xanh hoặc đỏ hoặc vàng.
Lấy được 21 viên bi trong đó không có bi xanh.

Nghiệm của đa thức là

-2
2
-1
Đa thức A(x) không có nghiệm.

Bậc của đa thức là:

-4
2
3
5

Trong tam giác ABC có góc A tù, trực tâm của tam giác ABC nằm ở vị trí

Bên trong tam giác
Bên ngoài tam giác
Trên một cạnh của tam giác
Trùng với đỉnh A của tam giác

Cho hình vẽ sau

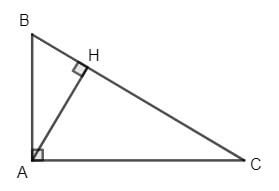
Khẳng định nào dưới đây là đúng?

Điểm B là hình chiếu của A trên đường thẳng BC
Đường vuông góc kẻ từ A đến đường thẳng BC là AH
AB < AH < BC
Điểm C là hình chiếu của B trên đường thẳng AC

Cho tam giác ABC có góc A là góc tù. Các đường trung trực của AB và AC cắt nhau tại O và lần lượt cắt BC tại E và F.

Xét tính đúng sai của các khẳng định sau:

Khẳng định	Đ/S
a) AB > BC	13.1
b) ∆EOA = ∆EOB	13.2
c) ∆OBC cân	13.3
d) AO là tia phân giác của góc EAF	13.4

Cho hai đa thức M(x) = 2 - 5x² + 3x⁴ + 4x² + 2x + x⁴ - 7x⁶ và N(x) = 7x⁶ - 4x⁴ - 3

Xét tính đúng sai của các khẳng định sau:

Khẳng định	Đ/S
a) Thu gọn và sắp xếp đa thức M(x) theo lũy thừa giảm dần của biến ta được M(x) = - 7x⁶+ 4x⁴ - x² + 2x + 2	14.1
b) Bậc của đa thức M(x) là 6	14.2
c) Đa thức G(x) = M(x) + N(x) khi đó G(x) = 14x⁶ + 8x⁴ + 2x + 5	14.3
d) Nghiệm của đa thức G(x) là x = 1	14.4

Một cửa hàng có một số lít nước mắm đựng đầy trong các thùng, mỗi thùng chứa được 20l. Nếu đổ số nước mắm vào các can mỗi can 5l thì số can 5l cần dùng phải nhiều hơn số thùng 20l là 30 cái. Hỏi cửa hàng có tất cả bao nhiêu lít nước mắm?

Đáp án: Cửa hàng có lít nước mắm.

Mỗi xúc xắc có 6 mặt, số chấm ở mỗi mặt tương ứng với các số 1; 2; 3; 4; 5; 6. Gieo ngẫu nhiên xúc xắc 1 lần.

Có bao nhiêu kết quả có thể xảy ra đối với biến cố "Số chấm xuất hiện là số chính phương".

Đáp án: Có kết quả.

Tính xác suất của biến cố "Mặt xuất hiện không nhỏ hơn 5".

Đáp án: Xác suất của biến cố "Mặt xuất hiện không nhỏ hơn 5" là . (Đáp án viết dưới dạng phân số tối giản a/b)

Cho tam giác ABC vuông tại A (AB > AC). Kẻ AH vuông góc với BC (H ∈ BC). Lấy điểm D thuộc tia đối của tia HA sao cho HD = HA.

Điền vào ô trống để hoàn thành phép chứng minh △CAH = △CDH.

△ABC vuông tại A (AB > AC)

Kẻ AH vuông góc với BC (H ∈ BC)

Lấy điểm D thuộc tia đối của tia HA sao cho HD = HA.

△CAH = △CDH

Xét △CAH và △CDH có:

18.1°

AH = 18.2 (gt)

Cạnh 18.3 chung

Suy ra △CAH = △CDH (18.4). (đpcm)

Qua D kẻ đường thẳng song song với AC cắt BC ở M và cắt AB ở K. So sánh độ dài các đoạn thẳng DM, DH, AB.

DM > DH > AB
AB > DM > DH
AB < DM < DH
DM < DH < AB

Kẻ BN vuông góc với đường thẳng AM (N thuộc tia AM). Điền vào ô trống để hoàn thành phép chứng minh .

Chứng minh:

+) Ta có DK // 20.1 (gt)

Mà 20.2 ⊥ AB

Suy ra

Tam giác BAD có đường cao BH và DK cắt nhau tại 20.3

Suy ra 20.4 là trực tâm của tam giác BAD

Suy ra AM ⊥ 20.5

Mà AM ⊥ BN (theo cách dựng)

Suy ra B, N, 20.6 thẳng hàng

Suy ra

+) Xét △ABC và △DCB có:

AB = 20.7 ( theo ý trước)

Cạnh 20.8 chung

AC = 20.9 (do BC là đường trung trực của AD)

Suy ra △ABC = △20.10 (c.c.c)

Suy ra

Từ (1) và (2) suy ra . (đpcm)

Tính giá trị của biểu thức tại x = 9.

Đáp án: Với x = 9 thì A = .