Đề thi thử môn Toán vào lớp 10 Sở TPHCM năm 2026

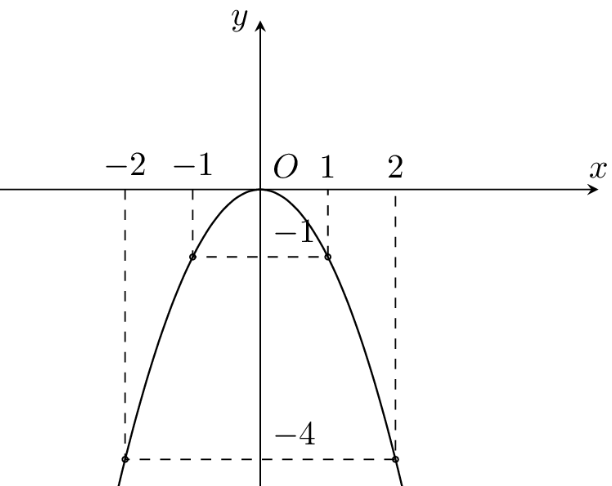
Cho hàm số có đồ thị là parabol .

a) Đồ thị  của hàm số trên là

b) Tìm điểm trên đồ thị  có hoành độ và tung độ đều dương sao cho  là hình vuông với  là điểm đối xứng của điểm qua , hai điểm và  là hình chiếu của và  lên trục hoành.

Trả lời: Điểm có hoành độ 2.1; tung độ  2.2.

Cho phương trình .

a) Khẳng định nào sau đây là đúng?

b) Không giải phương trình, tính giá trị biểu thức .

Trả lời: . (Kết quả viết dưới dạng phân số tối giản a/b)

Khi người ta kiểm tra lại thể tích thực của 1 lít xăng được mua từ các cửa hàng xăng dầu của hai thành phố A và B, kết quả được ghi lại trong biểu đồ sau:

a) Với những cửa hàng có thể tích thực đo được từ 980 ml trở lên sẽ được cho là sai số trong khoảng cho phép. Hỏi bao nhiêu cửa hàng có sai số nằm ngoài khoảng cho phép?

Trả lời: Có cửa hàng.

b) Anh Toàn đi xe máy và đổ xăng ở thành phố A, khi đến thành phố B, lại tiếp tục đổ xăng, mỗi cửa hàng xăng dầu anh Toàn vào đều là ngẫu nhiên. Hãy tính xác suất của biến cố M: “Cửa hàng xăng dầu anh Toàn vào đổ xăng có sai số trong khoảng cho phép” tại mỗi thành phố. (Kết quả viết dưới dạng phân số tối giản a/b)

Trả lời:

Tại thành phố A, P(M) = 6.1;

Tại thành phố B, P(M) = 6.2.

Để thiết kế mô hình đồ chơi có hình dạng con vịt như hình dưới, Nam thực hiện các bước sau:

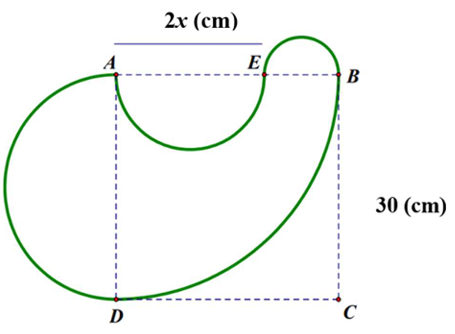
Bước 1. Phần thân vịt: Bạn Nam vẽ hình vuông  có cạnh dài  cm. Sau đó, Nam vẽ cung tròn  có tâm , vẽ nửa đường tròn đường kính  với  (cm).

Bước 2. Phần đầu và phần sau vịt: Bạn Nam vẽ nửa đường tròn đường kính  và nửa đường tròn đường kính .

(Cả bài lấy )

a) Viết biểu thức tính diện tích phần thân mô hình con vịt theo .

Đáp án: 7.1 7.2.

(Viết kết quả dưới dạng số thập phân nếu số không nguyên)

b) Tính diện tích mô hình con vịt, biết diện tích phần thân mô hình con vịt là .

Đáp án: .

(Viết kết quả dưới dạng số thập phân nếu số không nguyên)

Một hồ cá có hình dạng là một phần của hình cầu tâm . Hồ cá được đặt trên một giá đỡ như hình vẽ. Người ta đo được đường kính của miệng hồ là cm. Khoảng cách từ miệng hồ đến vị trí sâu nhất là cm.

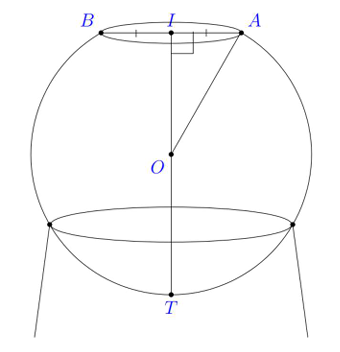
a) Tính bán kính của mặt cầu tạo nên hồ cá.

Đáp án: cm.

b) Người ta rót nước vào hồ sao cho mặt nước cách miệng hồ cm. Tính thể tích nước rót vào (kết quả làm tròn đến chữ số thập phân thứ nhất, đơn vị lít).

Đáp án: lít.

Hai xe bus đi trên tuyến đường như hình vẽ theo lộ trình từ hay , chạy liên tục không nghỉ và hết lộ trình lại tiếp tục một lộ trình nữa. Cùng một thời điểm, nếu hai xe bus cùng xuất phát từ và đi khác tuyến nhau thì sau giờ sẽ gặp nhau; còn nếu đi cùng tuyến nhau thì xe bus thứ hai sẽ vượt xe bus thứ nhất sau giờ. Tính thời gian ít nhất mà mỗi xe đi được từ đến , giả sử rằng vận tốc của các xe bus là không đổi trên các đoạn đường của lộ trình.

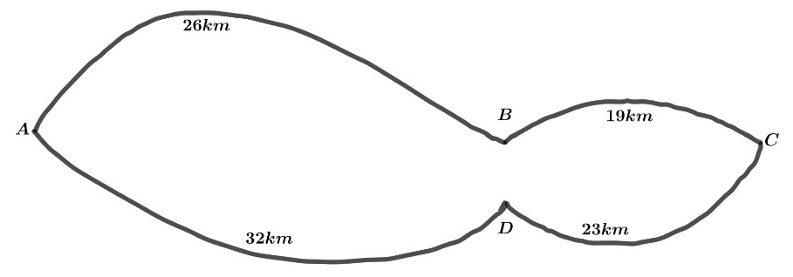
Trả lời: (Viết kết quả dưới dạng số thập phân nếu số không nguyên)

- Thời gian ít nhất của xe thứ nhất là 11.1 giờ;

- Thời gian ít nhất của xe thứ hai là 11.2 giờ.

Cho tam giác vuông tại () có là đường cao. Lần lượt vẽ đường tròn đường kính và đường tròn đường kính . Đường tròn cắt tại , đường tròn cắt tại . Đường trung tuyến của tam giác cắt tại .

a) Chứng minh tứ giác là hình chữ nhật.

Điền vào ô trống để hoàn thành bài chứng minh dưới đây:

Ta có 12.1° (góc nội tiếp chắn nửa đường tròn).

Suy ra 12.2 tại và 12.3 tại . 

Suy ra 12.4°.

Tứ giác có  12.5° 

Suy ra là hình chữ nhật. (đpcm)

b) Chứng minh là tiếp tuyến chung của đường tròn và .

Điền vào ô trống để hoàn thành bài chứng minh dưới đây:

+) Vì tứ giác là hình chữ nhật nên nội tiếp một đường tròn

(hai góc nội tiếp cùng chắn cung 13.1)

+) Ta có nên cân tại 13.2

góc 13.3  (1)

+) Lại có:  13.4 (cmt) và (gt)

Nên 13.5

(hai góc 13.6đồng vịtrong cùng phíaso le trong)  (2)

+) Từ (1) và (2)  góc 13.7. Do đó:

13.8° ( vuông tại 13.9)

13.10 tại ()

Vậy là tiếp tuyến của đường tròn   (3)

+) Chứng minh hoàn toàn tương tự, ta cũng có 13.11°

13.12 tại ()

Vậy là tiếp tuyến của đường tròn   (4)

Từ (3) và (4) suy ra là tiếp tuyến chung của đường tròn và . (đpcm)

c) Cho biết , . Tính diện tích tam giác . (Kết quả làm tròn đến hàng phần trăm, chỉ làm tròn sau bước tính cuối cùng)

Trả lời: .