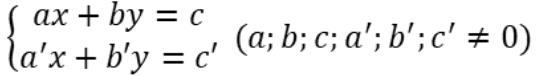Các bài toán giải hệ phương trình lớp 9

Bài toán giải hệ phương trình lớp 9 là một trong những dạng bài thường gặp khi ôn luyện toán vào lớp 10. Bài viết sau đây TAK12 sẽ chia sẻ phương pháp giải các dạng bài toán giải hệ phương trình lớp 9 cùng bài tập minh họa. Các em học sinh hãy đón đọc nhé!

1. Dạng 1: Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế

Quy tắc thế dùng để biến đổi một hệ phương trình thành hệ phương trình tương đương. Quy tắc thế gồm hai bước sau:

• Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thứ nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).
• Bước 2: Dùng phương trình mới ấy để thay thế cho phương trình thứ hai trong hệ (phương trình thứ nhất cũng thường được thay thế bởi hệ thức biểu diễn một ẩn theo ẩn kia có được ở bước 1).

Bài tập minh họa

Ví dụ: Giải hệ phương trình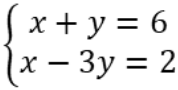

Hướng dẫn giải

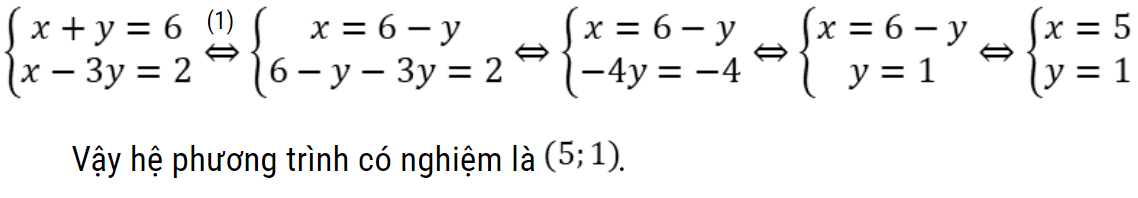
Giải thích: (1) Từ phương trình đầu ta biểu diễn x theo y, lấy kết quả đó thế vào x trong phương trình thứ hai.

Bài tập giải hệ phương trình bậc nhất hai ẩn bằng phương pháp thế

[%Included.Dangky%]

[%Included.Lớp 9%]

2. Dạng 2: Giải hệ phương trình bậc hai hai ẩn bằng phương pháp thế

Phương pháp 1: Thay một hằng số bởi một biểu thức

Bài tập minh họa

Ví dụ 1: Giải hệ phương trình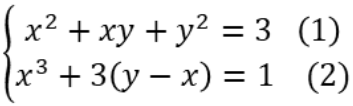

Hướng dẫn giải

Phương pháp 2: Thay một ẩn số bởi một biểu thức

Bài tập minh họa

Ví dụ 2: Giải hệ phương trình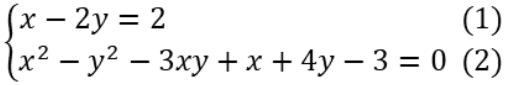

Hướng dẫn giải

Phương pháp 3: Thay một biểu thức bởi một hằng số

Bài tập minh họa

Ví dụ 3: Giải hệ phương trình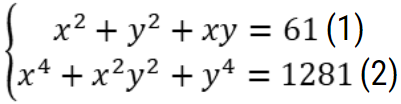

Hướng dẫn giải

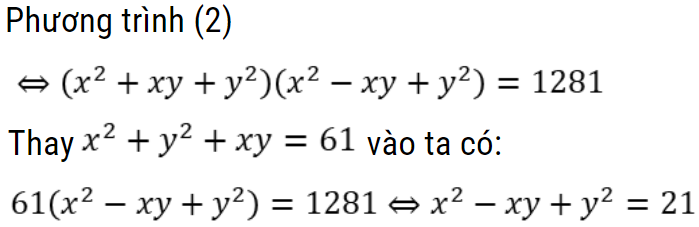
Bài tập giải hệ phương trình bậc hai hai ẩn bằng phương pháp thế

3. Dạng 3: Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số

Quy tắc cộng đại số dùng để biến đổi một hệ phương trình thành hệ phương trình tương đương. Quy tắc cộng đại số gồm hai bước sau:

• Bước 1: Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để được một phương trình mới.
• Bước 2: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia).

Bài tập minh họa

Ví dụ: Giải hệ phương trình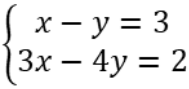

Hướng dẫn giải

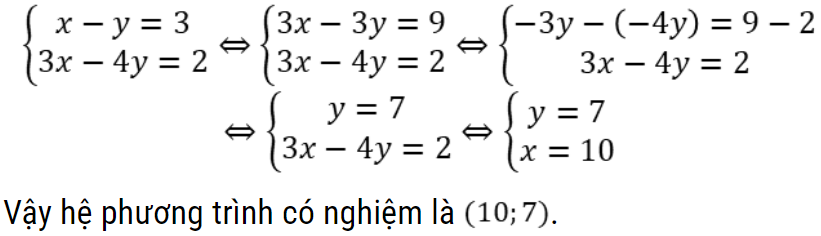
Bài tập giải hệ phương trình bậc hai hai ẩn bằng phương pháp cộng đại số

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

4. Dạng 4: Bài toán đặt ẩn phụ đưa về hệ phương trình bậc nhất hai ẩn

Phương pháp giải

• Bước 1: Đặt điều kiện để hệ có nghĩa.
• Bước 2: Đặt ẩn phụ và điều kiện của ẩn phụ.
• Bước 3: Giải hệ theo các ẩn phụ đã đặt (sử dụng phương pháp thế hoặc phương pháp cộng đại số).
• Bước 4: Trở lại ẩn ban đầu để tìm nghiệm của hệ.

Bài tập minh họa

Ví dụ: Giải hệ phương trình sau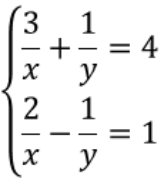

Hướng dẫn giải

Bài tập đặt ẩn phụ đưa về hệ phương trình bậc nhất hai ẩn

5. Dạng 5: Bài toán biến đổi đưa về hệ phương trình bậc nhất hai ẩn

Phương pháp giải

• Bước 1: Nhân khai triển, chuyển vế đưa hệ phương trình về hệ phương trình bậc nhất hai ẩn.
• Bước 2: Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.
• Bước 3: Kết luận.

Bài tập minh họa

Ví dụ: Giải hệ phương trình sau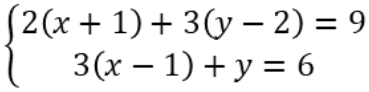

Hướng dẫn giải

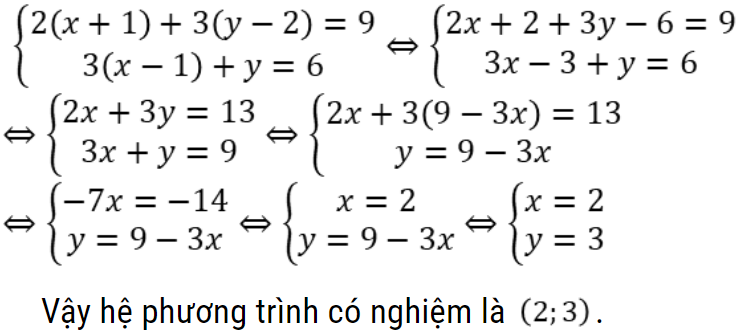
Bài tập biến đổi đưa về hệ phương trình bậc nhất hai ẩn

6. Dạng 6: Bài toán giải hệ phương trình lớp 9 chứa dấu giá trị tuyệt đối

Để giải hệ phương trình chứa dấu giá trị tuyệt đối chúng ta có thể sử dụng phương pháp xét dấu.

Có: l A l = B

• Với A ≥ 0 thì A = B
• Với A < 0 thì A = -B

Bài tập minh họa

Ví dụ: Giải hệ phương trình sau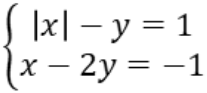

Hướng dẫn giải

Bài tập giải hệ phương trình lớp 9 chứa dấu giá trị tuyệt đối

7. Dạng 7: Hệ phương trình bậc nhất hai ẩn chứa tham số

7.1. Giải hệ phương trình theo tham số m cho trước

Phương pháp giải

• Bước 1: Thay giá trị của m vào hệ đã cho.
• Bước 2: Giải hệ phương trình vừa nhận được theo các phương pháp đã biết.
• Bước 3: Kết luận.

Bài tập minh họa

Ví dụ: Cho hệ phương trình 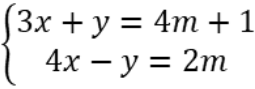. Giải hệ phương trình với m = 1.

Hướng dẫn giải

7.2. Tìm m để hệ phương trình có nghiệm (x; y) thỏa mãn điều kiện cho trước

Phương pháp giải

• Bước 1: Giải hệ phương trình tìm nghiệm (x; y) theo tham số m.
• Bước 2: Thế nghiệm (x; y) vào biểu thức điều kiện cho trước rồi giải tìm m.
• Bước 3: Kết luận giá trị của m.

Bài tập minh họa

Ví dụ: Cho hệ phương trình ảnh 7.2 Bài tập minh họa. Tìm m để hệ phương trình có nghiệm (x; y) thỏa mãn x + y = 4.

Hướng dẫn giải

7.3. Tìm mối liên hệ giữa x và y không phụ thuộc vào tham số m

Phương pháp 1:

• Bước 1: Giải hệ phương trình tìm nghiệm (x; y) theo tham số m.
• Bước 2: Dùng phương pháp thế hoặc cộng đại số làm mất tham số m.
• Bước 3: Kết luận.

Bài tập minh họa

Ví dụ 1: Cho hệ phương trình 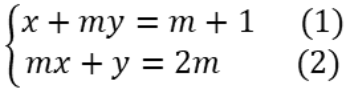. Tìm hệ thức liên hệ giữa x, y không phụ thuộc vào giá trị của m.  

Hướng dẫn giải

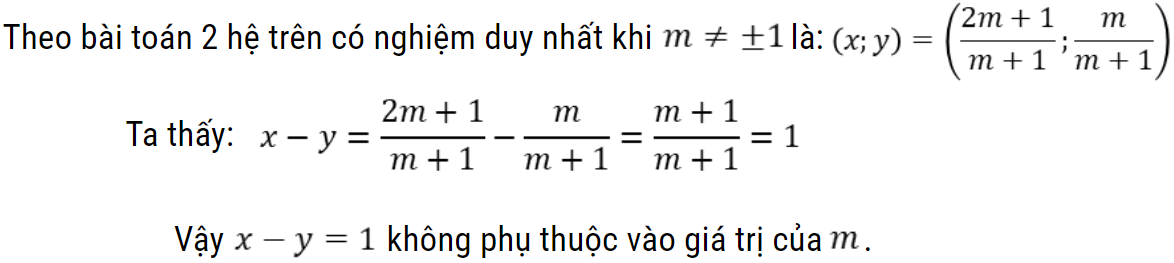
Phương pháp 2:

• Bước 1: Đưa hệ phương trình về dạng cm + d = f(x, y), c'm + d' = g(x, y).
• Bước 2: Dùng phương pháp cộng để khử m sẽ nhận được biểu thức liên hệ giữa x, y không phụ thuộc m.
• Bước 3: Kết luận.

Bài tập minh họa

Ví dụ 2: Cho hệ phương trình 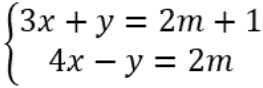. Tìm hệ thức liên hệ giữa x, y không phụ thuộc vào giá trị của m.  

Hướng dẫn giải

Bài tập giải hệ phương trình bậc nhất hai ẩn chứa tham số

8. Dạng 8: Bài toán giải và biện luận hệ phương trình có tham số

Phương pháp 1

• Bước 1: Bằng phương pháp khử hoặc cộng đại số nhận được phương trình bậc nhất có dạng ax + b = 0
• Bước 2: Xét phương trình bậc nhất: ax + b = 0 (với a, b là hằng số) (*).

- TH1: Nếu a ≠ 0 thì phương trình (*) có nghiệm duy nhất x = -b/a, từ đó tìm y.
- TH2: Nếu a = 0, b ≠ 0 thì phương trình (*) vô nghiệm.
- TH3: Nếu a = 0, b = 0 thì phương trình (*) vô số nghiệm.

• Bước 3: Kết luận nghiệm của hệ phương trình.
  

Bài tập minh họa

Ví dụ 1: Cho hệ phương trình 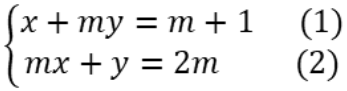. Giải và biện luận hệ phương trình theo tham số m.

Hướng dẫn giải

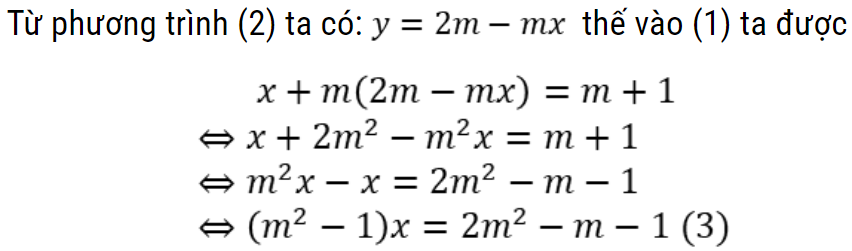
Phương pháp 2: Hệ phương trình

• Hệ phương trình có nghiệm duy nhất nếu
• Hệ phương trình vô nghiệm nếu
• Hệ phương trình có vô số nghiệm nếu

Bài tập minh họa

Ví dụ 2: Cho hệ phương trình 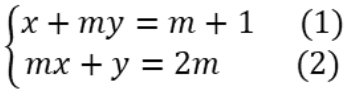. Biện luận số nghiệm của hệ phương trình theo tham số m.

Hướng dẫn giải

Bài tập giải và biện luận hệ phương trình có tham số

9. Dạng 9: Bài toán giải hệ phương trình đối xứng loại 1

Định nghĩa: Hệ phương trình đối xứng loại 1 là hệ phương trình mà khi ta thay đổi vai trò x, y cho nhau thì mỗi phương trình của hệ không thay đổi.

Ví dụ: 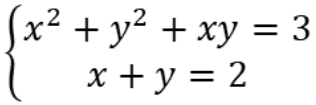là một hệ phương trình đối xứng loại 1.

Một số biểu diễn biểu thức đối xứng qua S và P

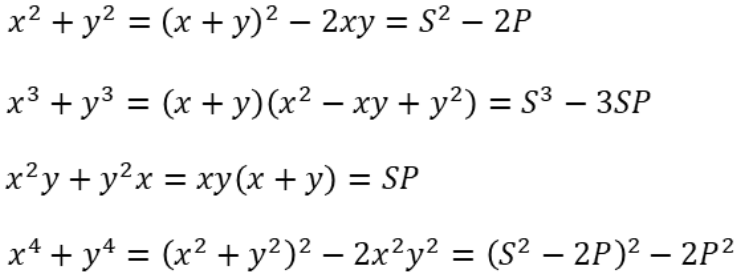
Bài tập minh họa

Ví dụ: Giải hệ phương trình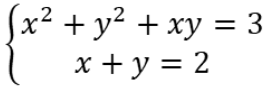

Hướng dẫn giải

Bài tập giải hệ phương trình đối xứng loại 1

10. Dạng 10: Bài toán giải hệ phương trình đối xứng loại 2

Định nghĩa: Hệ phương trình đối xứng loại 2 là hệ phương trình mà khi ta thay đổi vai trò x, y cho nhau thì hai phương trình trong hệ sẽ hoán đổi cho nhau.

Hệ đối xứng loại 2 có dạng:

Ví dụ: 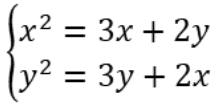là một hệ phương trình đối xứng loại 2.

Bài tập minh họa

Ví dụ: Giải hệ phương trình .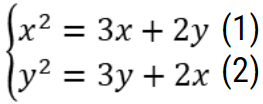

Hướng dẫn giải

Bài tập giải hệ phương trình đối xứng loại 2

11. Dạng 11: Bài toán giải hệ phương trình đẳng cấp bậc 2

Định nghĩa: Hệ phương trình đẳng cấp là hệ gồm 2 phương trình 2 ẩn mà ở mỗi phương trình bậc của mỗi ẩn bằng nhau.

Hệ đẳng cấp có dạng: , trong đó f, g là các hàm số cùng bậc.

Ví dụ: 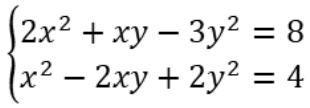là một hệ phương trình đẳng cấp bậc 2.

Bài tập minh họa

Ví dụ: Hệ phương trình 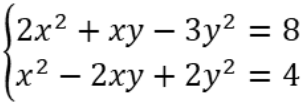có bao nhiêu nghiệm?

Hướng dẫn giải

Bài tập giải hệ phương trình đẳng cấp bậc 2

Nội dung vừa rồi đã chia sẻ phương pháp giải các dạng bài toán giải hệ phương trình lớp 9 thường gặp nhất, đi kèm với bài tập minh họa có lời giải chi tiết. Mong rằng với những thông tin trên, các em học sinh lớp 9 có thể ôn luyện dạng toán này thành thạo để nắm vững kiến thức thi vào lớp 10.

[%Included.TAK12%]