Ôn tập bất đẳng thức côsi lớp 9

Sử dụng bất đẳng thức Côsi là phương pháp giải các bài toán chứng minh bất đẳng thức thường xuyên xuất hiện trong đề thi vào 10 môn Toán. Cùng TAK12 tìm hiểu về lý thuyết bất đẳng thức Côsi lớp 9 và các bài tập áp dụng bất đẳng thức Côsi trong bài viết sau.

1. Kiến thức cần nhớ về bất đẳng thức Côsi lớp 9

1.1. Lý thuyết bất đẳng thức Côsi lớp 9

1.2. Chứng minh bất đẳng thức Côsi với hai số thực a và b không âm

Với a = 0, b = 0 thì bất đẳng thức luôn luôn đúng.

Với a, b > 0, ta chứng minh:

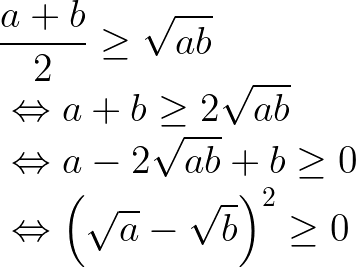
Vậy: Bất đẳng thức luôn đúng với mọi a, b không âm.

[%Included.Lớp 9%]

1.3. Hệ quả của bất đẳng thức Côsi

Hệ quả 1: Nếu tổng hai số dương không đổi thì tích của chúng lớn nhất khi hai số đó bằng nhau

Hệ quả 2: Nếu tích hai số dương không đổi thì tổng của của hai số này nhỏ nhất khi hai số đó bằng nhau

[%Included.Dangky%]

2. Hướng dẫn giải bài toán về bất đẳng thức Côsi lớp 9

Bài 1: Tìm giá trị nhỏ nhất của biểu thức 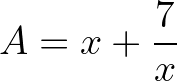với x > 0

Hướng dẫn giải

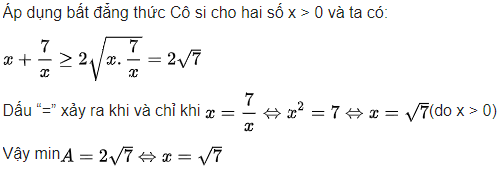
Bài 2: Cho x > 0, y > 0 thỏa mãn điều kiện 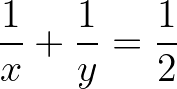. Tìm giá trị lớn nhất của biểu thức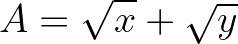

Hướng dẫn giải

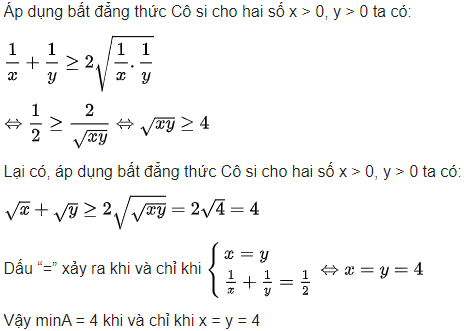
Bài 3: Cho a, b, c > 0, chứng minh rằng: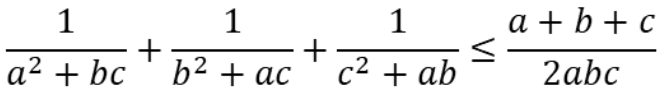

Hướng dẫn giải

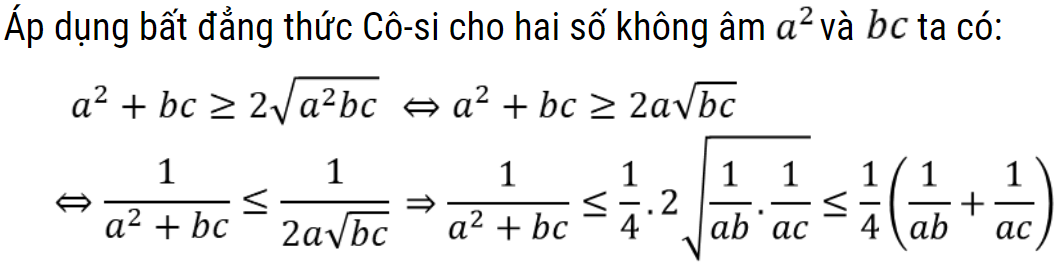
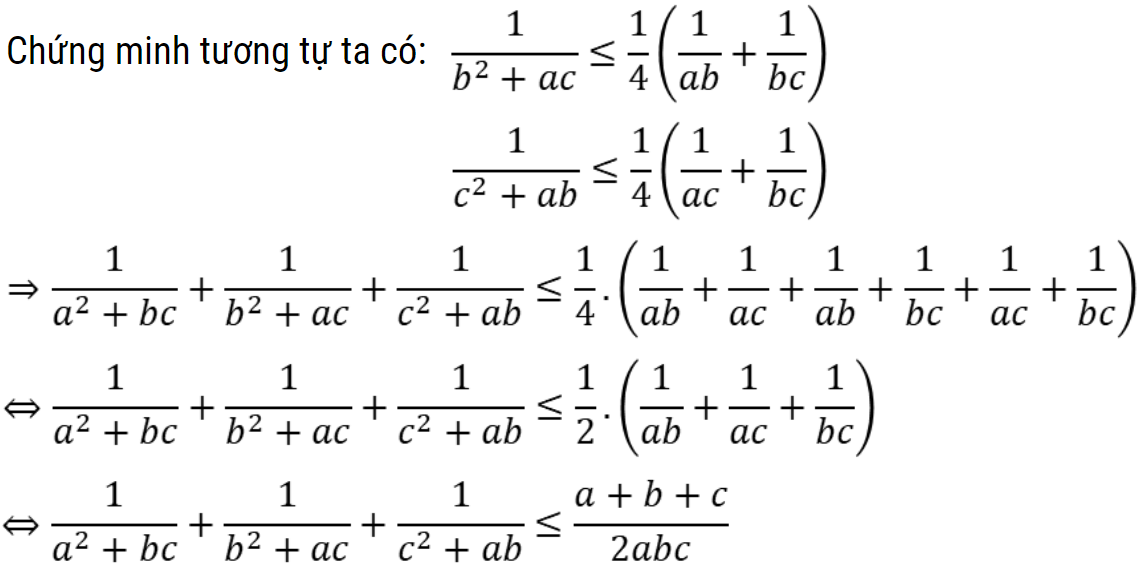
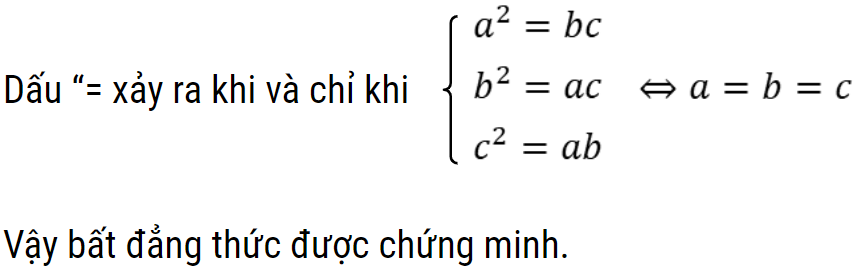
Bài 4: Chứng minh với ba số a, b, c không âm thỏa mãn a + b + c = 3 thì:

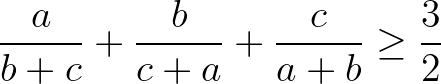
Hướng dẫn giải

Áp dụng bất đẳng thức Cô si cho ba số a, b, c không âm có:

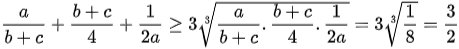
Tương tự, ta có:

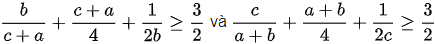
Cộng vế với vế, ta có:

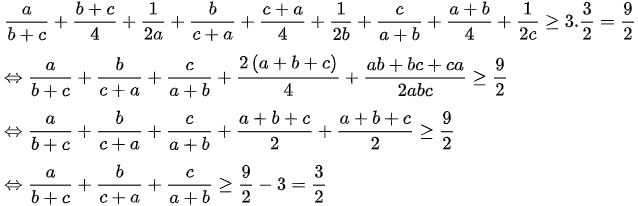
Dấu "=" xảy ra khi và chỉ khi a = b = c = 1

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

3. Bài tập tự luyện về bất đẳng thức Côsi lớp 9

Bài 1: Cho ba số thực dương x, y, z. Chứng minh rằng:

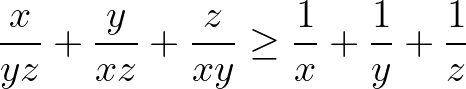
Gợi ý giải: Chứng minh 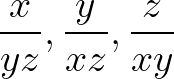là các số dương. Sau đó, áp dụng bất đẳng thức Côsi lần lượt các cặp số .

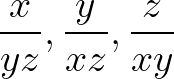Bài 2: Cho ba số thực dương a, b, c thỏa mãn a + b + c = 1. Chứng minh rằng:

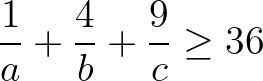
Gợi ý giải: Chứng minh 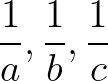là các số dương. Sau đó, áp dụng bất đẳng thức Côsi 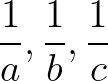lần lượt từng phân số với 36a, 36b và 36c.

Bài 3: Tìm giá trị nhỏ nhất của biểu thức

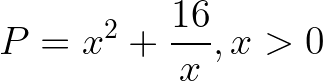
Gợi ý giải: Tách 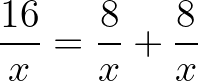. Sau đó áp dụng Côsi cho 3 số .

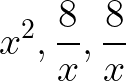Bài 4: Trong các hình chữ nhật có chu vi bằng 300m, hình chữ nhật có diện tích lớn nhất bằng bao nhiêu?

Gợi ý giải: Ta có a + b = 300 : 2 = 150 (m). Giả sử hình chữ nhật có chiều dài và chiều rộng lần lượt là a, b (0 < a, b < 150) (đơn vị: mét). Sau đó áp dụng bất đẳng thức Côsi cho độ dài hai cạnh a và b.

Bài 5: Với a, b, c là các số thực không âm, chứng minh:

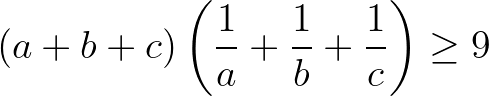
Gợi ý giải: Áp dụng bất đẳng thức Côsi cho ba số a, b, c không âm.

👉 Thực hành thêm: Bài tập chứng minh bất đẳng thức bằng Côsi, Bu-nhi-a-cop-sky,...

Như vậy, bài viết trên đã giới thiệu đầy đủ lý thuyết về bất đẳng thức Côsi lớp 9, cũng như cách làm các bài tập vận dụng bất đẳng thức Côsi. Hy vọng các bạn ghi nhớ và áp dụng hiệu quả vào các bài toán cụ thể trong quá trình ôn thi vào 10.

[%Included.TAK12%]