Ôn tập nguyên lý Dirichlet lớp 9

Nguyên lý Dirichlet lớp 9 là một trong những nguyên lý được vận dụng để giải rất nhiều bài toán số học, đại số, hình học khi ôn thi toán vào 10. Cùng TAK12 tìm hiểu những kiến thức cần nhớ về nguyên lý Dirichlet và phương pháp giải các dạng toán về nguyên lý Dirichlet trong bài viết sau.

1. Kiến thức cần nhớ về nguyên lý Dirichlet lớp 9

1.1. Nội dung nguyên lý Dirichlet

Nguyên lý Dirichlet được phát biểu như sau: Không thể nhốt 7 con thỏ vào 3 cái lồng mà mỗi cái lồng có không quá 2 con thỏ. Nói cách khác, nếu nhốt 7 con thỏ vào 3 cái lồng thì tồn tại ít nhất một lồng có từ 3 con trở lên.

Tổng quát

Nếu có k lồng để nhốt m con thỏ (với m = kn + r (0 < r ≤ k - 1)) thì tồn tại ít nhất một lồng có chứa từ n + 1 con thỏ trở lên.

Chứng minh

Giả sử ngược lại mỗi chuồng chứa không quá m con thỏ thì tổng số thỏ nhốt trong n chuồng sẽ không quá m.n con thỏ: Mâu thuẫn với giả thiết là số thỏ bằng m.n + r. Vậy phải có ít nhất một chuồng chứa không ít hơn m + 1 con thỏ.

1.2. Một số dạng áp dụng của nguyên lý Dirichlet

a) Nguyên lý Dirichlet cơ bản: Nếu nhốt n + 1 con thỏ vào n cái chuồng thì bao giờ cũng có một chuồng chứa ít nhất hai con thỏ.

b) Nguyên lý Dirichlet tổng quát: Nếu có N đồ vật được đặt vào trong k hộp thì sẽ tồn tại một hộp chứa ít nhất đồ vật.

c) Nguyên lí Dirichlet mở rộng: Nếu nhốt n con thỏ vào m ≥ 2 cái chuồng thì tồn tại một chuồng có ít nhất 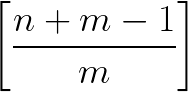con thỏ.

d) Nguyên lí Dirichlet dạng tập hợp: Cho A và B là hai tập hợp khác rỗng có số phần tử hữu hạn, mà số lượng phần tử của A lớn hơn số lượng phần tử của B. Nếu với một quy tắc nào đó, mỗi phần tử của A cho tương ứng với một phần tử của B, thì tồn tại ít nhất hai phần tử khác nhau của A mà chúng tương ứng với một phần tử của B.

1.3. Phương pháp ứng dụng nguyên lý Dirichlet

Bản thân nguyên lí Dirichlet khá đơn giản và dễ hiểu, tuy nhiên việc ứng dụng nguyên lí này lại không hề đơn giản. Để sử dụng nguyên lý Dirichlet ta phải làm xuất hiện tình huống nhốt “thỏ” vào “chuồng” và thoả mãn các điều kiện:

• Số “thỏ” phải nhiều hơn số chuồng.
• “Thỏ” phải được nhốt hết vào các “chuồng”, nhưng không bắt buộc chuồng nào cũng phải có thỏ.

[%Included.Dangky%]

[%Included.Lớp 9%]

2. Hướng dẫn giải các dạng bài toán về nguyên lý Dirichlet lớp 9

2.1. Dạng 1: Bài toán chia hết

Phương pháp giải: Thông thường ta coi m số tự nhiên đã cho là m “con thỏ”, các số dư trong phép chia các số tự nhiên đó cho n là những “lồng”; như vậy sẽ có n cái lồng: lồng i (0 ≤ i ≤ b) gồm những số tự nhiên đã cho chia cho n dư i.

Bài tập minh họa

Bài 1: Chứng minh rằng:

a) Trong 2012 số tự nhiên bất kì luôn tìm được hai số chia cho 2011 có cùng số dư (hay hiệu của chúng chia hết cho 2011).

b) Trong 2012 số tự nhiên bất kì luôn tìm được một số chia hết cho 2012 hoặc luôn tìm được hai số chia cho 2012 có cùng số dư

Hướng dẫn giải

a) Ta coi 2012 số tự nhiên đã cho là 2012 “con thỏ”; “lồng i” gồm các số chia cho 2011 dư i (0 ≤ i ≤ 2011) nên có 2011 lồng: lồng 0, lồng 1, …, lồng 2010. Như vậy có 2011 lồng chứa 2012 con thỏ nên theo nguyên lí Dirchlet tồn tại ít nhất một lồng chứa không ít hơn hai con thỏ, tức là có ít nhất hai số chia cho 2011 có cùng số dư.

b) Nếu trong 2012 số đã cho có ít nhất một số chia hết cho 2012 thì ta chọn luôn số này. Nếu không có số nào chia hết cho 2012 thì khi chia cho 2012 nhận nhiều nhất 2012 số dư khác nhau là 1, 2, …, 2011. Theo nguyên lí Dirichlet, tồn tại ít nhất hai số chia cho 2012 có cùng số dư.

Nhận xét: Ta có thể tổng quát bài toán trên như sau:

1. Trong n + 1 số tự nhiên bất kì luôn tìm được hai số chia cho n có cùng số dư (hay hiệu của chúng chia hết cho n).
2. Trong n số tự nhiên bất kì luôn tìm được một số chia hết cho n hoặc luôn tìm được hai số chia cho n có cùng số dư.

Bài 2: Chứng minh rằng luôn tìm được số có dạng 20122012…2012 (gồm các số 2012 viết liên tiếp nhau) chia hết cho 2013.

Hướng dẫn giải

Xét 2014 số sau: 2012, 20122012, ..., 2012...2012 (gồm 2014 bộ số 2102).

Đem 2014 số này lần lượt chia cho 2013, có 2014 số mà chỉ có 2013 số dư trong phép chia cho 2013 (là 0, 1, 2, ..., 2012) nên luôn tồn tại hai số chia cho 2013 có cùng số dư, chẳng hạn đó là a = 2012...2012 (gồm i bộ 2012) và b = 2012...2012 (gồm j bộ 2012) với 1 ≤ i ≤ j ≤ 2014.

Khi đó:

b - a = 2012...2012.10⁴ⁱ (gồm j – i bộ 2012) sẽ chia hết cho 2013.

Lại có ƯCLN (10⁴ⁱ, 2013) = 1 nên số 2012...2012 (gồm j – i bộ 2012) sẽ chia hết cho 2013. Bài toán được chứng minh.

(Ở đây “thỏ” là số có dạng 2012...2012, “lồng” là số dư trong phép chia cho 2013).

Nhận xét: Mấu chốt của bài toán là chọn ra 2014 (= 2013 + 1) số tự nhiên có dạng đã cho. Từ đó ta có thể phát biểu nhiều bài toán tương tự, chẳng hạn như: Chứng minh rằng luôn tìm được số có dạng 111...1 chia hết cho 29.

2.2. Dạng 2: Bài toán về tính chất các phần tử trong tập hợp

Phương pháp giải: Thông thường ta phải lập ra những tập hợp có tính chất cần thiết rồi sử dụng nguyên lí Dirichlet để chứng tỏ có hai phần tử thuộc hai tập hợp bằng nhau.

Bài tập minh họa

Cho sáu số nguyên dương đôi một khác nhau và đều nhỏ hơn 10. Chứng minh rằng luôn tìm được 3 số trong đó có một số bằng tổng hai số còn lại.

Hướng dẫn giải

Gọi sáu số nguyên dương đã cho là a₁, a₂, a₃, a₄, a₅, a₆ với 0 < a₁ < a₂ < ... < a₆ < 10.

Đặt A = {a₂, a₃, a₄, a₅, a₆} gồm 5 phần tử có dạng a_m với m ∈ {2, 3, 4, 5, 6}. 

Đặt B = {a₂ - a₁; a₃ - a₁; a₄ - a₁; a₅ - a₁; a₆ - a₁} gồm 5 phần tử có dạng a_n - a₁ với n ∈ {2, 3, 4, 5, 6}.

Ta thấy các phần tử của hai tập hợp A và B đều thuộc tập hợp gồm 9 phần tử {1, 2, 3, ..., 9} trong khi tổng số phần tử của hai tập hợp A và B là 5 + 5 = 10.

Theo nguyên lí Dirichlet tồn tại hai số bằng nhau mà chúng không thể thuộc cùng một tập hợp, nên có một số thuộc tập hợp A bằng một số thuộc tập hợp B, tức là a_m = a_n - a₁, do đó a_n = a_m + a₁.

Ba số a_m, a_n, a₁ đôi một khác nhau. Thật vậy, a_m ≠ a_n vì nếu a_m = a_n thì a₁ = 0 trái với giả thiết của bài toán.

Vậy tồn tại ba số a_m, a_n, a₁ trong các số đã cho mà a_n = a_m + a₁ (đpcm)

(Ở đây, có 10 “thỏ” là 10 số a₁, a₂, a₃, a₄, a₅, a₆, a₂ - a₁; a₃ - a₁; a₄ - a₁; a₅ - a₁; a₆ - a₁ và có 9 “lồng” là 9 số 1, 2, 3, 4, 5, 6, 7, 8, 9).

Nhận xét: Để giải bài toán này, ta cần tạo ra hai tập hợp gồm các phần tử nhỏ hợn 10 và tổng số phần tử của hai tập hợp phải không nhỏ hơn 10. Từ đó suy ra tồn tại hai phần tử của hai tập hợp bằng nhau.

2.3. Dạng 3: Bài toán liên quan đến bảng ô vuông

Phương pháp giải:

• Một bảng vuông kích thước n x n gồm n dòng, n cột và 2 đường chéo. Mỗi dòng, mỗi cột, mỗi đường chéo đều có n ô vuông.
• Một bảng các ô vuông kích thước m x n gồm m dòng và n cột.

Bài tập minh họa

Bài 1: Cho một mảng ô vuông kích thước 5 x 5. Người ta viết vào mỗi ô của bảng một trong các số -1, 0, 1; sau đó tính tổng của các số theo từng cột, theo từng dòng và theo từng đường chéo. Chứng minh rằng trong tất cả các tổng đó luôn tồn tại hai tổng có giá trị bằng nhau.

Hướng dẫn giải

Bảng ô vuông kích thước 5 x 5 có 5 dòng, 5 cột, 2 đường chéo nên sẽ có 12 tổng của các số được tính theo dòng, theo cột và theo đường chéo. Mỗi dòng, cột và đường chéo đều có ghi 5 số thuộc tập {–1; 0; 1}.

Vì vậy giá trị mỗi tổng thuộc tập hợp {–5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5} có 11 phần tử. Có 12 tổng nhận trong tập 11 các giá trị khác nhau nên theo nguyên lí Dirichlet tồn tại ít nhất hai tổng nhận cùng một giá trị. Bài toán được chứng minh.

(Ở đây “thỏ” là tổng nên có 12 “thỏ”, “lồng” là giá trị của tổng nên có 11 “lồng”).

Nhận xét: Với cách giải tương tự, ta có bài toán tổng quát sau:

Cho một bảng ô vuông kích thước n x n. Người ta viết vào mỗi ô của bảng một trong các số –1, 0, 1; sau đó tính tổng của các số theo từng cột, theo từng dòng và theo từng đường chéo. Chứng minh rằng trong tất cả các tổng đó luôn tồn tại hai tổng có giá trị bằng nhau

Bài 2: Trên bảng ô vuông kích thước 8 x 8, ta viết các số tự nhiên từ 1 đến 64, mỗi số viết vào một ô một cách tùy ý. Chứng minh rằng luôn tồn tại hai ô vuông chung cạnh mà hiệu các số ghi trong chúng không nhỏ hơn 5.

Hướng dẫn giải

Ta xét hàng có ô ghi số 1 và cột có ô ghi số 64. Hiệu giữa hai ô này là 63.

Số cặp ô kề nhau từ ô ghi số 1 đến ô ghi số 64 nhiều nhất là 14 (gồm 7 cặp ô chung cạnh

tính theo hàng và 7 cặp ô chung cạnh tính theo cột).

Ta có 64 = 14.4 + 7 nên theo nguyên lí Dirichlet, tồn tại ít nhất hai ô kề nhau mà hai số ghi

trên đó có hiệu không nhỏ hơn 4 + 1 = 5. Bài toán được chứng minh.

(Ở đây, “thỏ” là hiệu của hai số trong 64 số (từ 1 đến 64) nên có 63 thỏ; “lồng” là số cặp ô vuông kề nhau từ ô ghi số 1 đến ô ghi số 64 nên có nhiều nhất là 14 lồng).

Nhận xét:

• Mấu chốt của bài toán là quan tâm đến hai ô vuông ghi số nhỏ nhất (số 1) và số lớn nhất (số 64) sẽ có hiện lớn nhất là 63; đồng thời xét từ ô ghi số 1 đến ô ghi số 64 chỉ cần tối đa là (8 – 1) + (8 – 1) = 14 ô.
• Ở đây ta đã vận dụng nguyên lí Dirichlet tổng quát: Nếu có k lồng để nhốt m con thỏ (với m = kn + r (0 < r ≤ k - 1)) thì tồn tại ít nhất một lồng có chứa từ n + 1 con thỏ trở lên.

2.4. Dạng 4: Bài toán liên quan đến thực tế

Phương pháp giải: Khi chứng minh sự tồn tại một số đối tượng thỏa mãn điều kiện nào đó, ta thường sử dụng nguyên lí Dirichlet. Điều quan trọng nhất là phải xác định được “thỏ” và “lồng”.

Bài tập minh họa

Bài 1: Một trường học có 1115 học sinh. Chứng tỏ rằng luôn có ít nhất 4 em có cùng ngày, tháng sinh.

Hướng dẫn giải

Ta chú ý ở đây có cụm từ  “4 em cùng ngày sinh” giống với 4 con thỏ nhốt trong cùng một lồng. Như vậy số thỏ ở đây là số học sinh (1115), số lồng là số ngày trong một năm (365). Mà 1115 = 365.3 + 20 nên tồn tại ít nhất 3+1= 4 học sinh cùng ngày tháng sinh.

Bài 2: Một tổ học tập có 10 học sinh. Khi viết chính tả, cả tổ đều mắc lỗi, trong đó bạn Bình mắc nhiều lỗi nhất (mắc 5 lỗi). Chứng minh rằng trong tổ ấy có ít nhất 3 bạn đã mắc một số lỗi bằng nhau.

Hướng dẫn giải

Ta coi “thỏ” là học sinh (trừ bạn Bình) nên có 9 thỏ; “lồng” là số lỗi chính tả học sinh mắc phải nên có 4 lồng: lồng i gồm những học sinh mắc i lỗi (i = 1, 2, 3, 4).

Có 9 thỏ nhốt vào 4 lồng, mà 9 = 4.2 + 1, nên theo nguyên lí Dirichlet tồn tại ít nhất một lồng chứa không ít hơn 2 + 1 = 3 thỏ, tức là có ít nhất 3 bạn mắc một số lỗi bằng nhau.

Bài 3: Ở một vòng chung kết cờ vua có 8 đấu thủ tham gia. Mỗi đấu thủ đều phải gặp đủ 7 đấu thủ còn lại, mỗi người một trận. Chứng minh rằng, trong mọi thời điểm giữa các cuộc đấu, bao giờ cũng có hai đấu thủ đã đấu một số trận như nhau

Hướng dẫn giải

Ta coi “thỏ” là đấu thủ nên có 8 thỏ; “lồng” là số trận đấu của đấu thủ nên có 8 lồng: “lồng i” gồm các đấu thủ đã thi đấu i trận (với i = 0, 1, 2, 3, 4, 5, 6, 7).

Ta thấy lồng 0 và lồng 7 không đồng thời tồn tại, vì nếu có một đấu thủ chưa đấu trận nào thì sẽ không có đấu thủ nào đã đấu đủ 7 trận, cũng như nếu có đấu thủ đã đấu đủ 7 trận thì không có ai chưa đấu trận nào.

Như vậy, có 7 lồng chứa 8 con thỏ nên theo nguyên lí Dirichlet tồn tại một lồng chứa không ít hơn 2 con thỏ, tức là trong mọi thời điểm giữa các cược đấu luôn tìm được 2 đấu thủ đã đấu dùng một số trận.

2.5. Dạng 5: Bài toán liên quan đến sự sắp xếp

Phương pháp giải: Các bài toán về sắp xếp chỗ, phân công việc không đòi hỏi nhiều về kiến thức và kĩ năng tính toán, chúng chủ yếu kết hợp suy luận lôgic để xét các khả năng có thể xảy ra với nguyên lí Dirichlet.

Bài tập minh họa

Bài 1: Có 20 người quyết định đi bơi thuyền bằng 10 chiếc thuyền đôi. Biết rằng nếu hai người A và B mà không quen nhau thì tổng số những người quen của A và những người quen của B không nhỏ hơn 19. Chứng minh rằng có thể phân công vào các thuyền đôi sao cho mỗi thuyền đều là hai người quen nhau.

Hướng dẫn giải

Nếu trong 20 người không có hai người nào quen nhau thì tổng số người quen của hai người bất kì là 0. Điều này mâu thuẫn với giả thiết là tổng số người quen của hai người không nhỏ hơn 19. Vậy tồn tại một số cặp quen nhau.

Ta xếp mỗi cặp quen nhau đó vào một thuyền đôi. Gọi k là số lượng thuyền lớn nhất mà trong đó ta có thể xếp được những cặp quen nhau vào một thuyền và kí hiệu thuyền thứ i xếp hai người Ai và Bi quen nhau (1 ≤ i ≤ k).

Giả sử k ≤ 9, kí hiệu tập hợp M gồm những người chưa được xếp vào thuyền nào, tức là gồm những người đôi một không quen nhau.

Chọn hai người A và B trong tập hợp M.

Theo bài ra thì tổng số người quen của A và số người quen của B không nhỏ hơn 19 và những người quen A hoặc quen B đã được xếp vào thuyền rồi.

Như vậy có 19 người quen hệ quen A hoặc B được xếp vào nhiều nhất là 9 thuyền đôi (trừ 1 thuyền vì A, B chưa được xếp), mà 19 = 9.2 + 1 nên theo nguyên lí Dirichlet tồn tại ít nhất một thuyền chở 2 người quen cả A và B.

Nhưng khi đó ta có thể xếp lại như sau: trong k – 1 thuyền đầu tiên vẫn giữ nguyên, còn thuyền thứ k xếp Ak và B, còn thuyền thứ k + 1 xếp A và Bk. Điều này mâu thuẫn với giả sử.

Theo cách xếp này ta tiếp tục xếp đến hết 10 thuyền sao cho mỗi thuyền hai người đều quen nhau.

Bài 2: Kì thi tuyển sinh vào trường THPT chuyên Long An năm nay có 529 học sinh đến từ 16 địa phương khác nhau tham dự. Gỉa sử điểm bài thi môn Toán của mỗi học sinh đều là số nguyên dương lớn hơn 4 và bé hơn hoặc bằng 10. Chứng minh rằng luôn tìm được 6 học sinh có điểm môn Toán giống nhau và cùng đến từ một địa phương.

Hướng dẫn giải

Ta có 529 học sinh có điểm bài thi 5 điểm đến 10 điểm. Theo nguyên lí Dirichlet ta có 89 học sinh có điểm bài thi như nhau (từ 5 điểm đến 10 điểm).

Ta có 89 học sinh có điểm bài thi như nhau và đến từ 16 địa phương. Theo nguyên lí Dirichlet tìm được 6 em có cùng điểm thi môn toán và đến từ cùng một địa phương

2.6. Dạng 6: Bài toán hình học

Phương pháp giải: Một số các dạng toán hình học thường gặp:

1. Nếu trên một đoạn thẳng độ dài 1 đặt một số đoạn thẳng có tổng độ dài lớn hơn 1 thì có ít nhất hai trong số các đoạn thẳng đó có điểm chung.
2. Nếu trên đường tròn có bán kính 1 đặt một số cung có tổng độ dài lớn hơn 2π thì có ít nhất hai trong số các cung đó có điểm chung.
3. Trong một hình có diện tích S đặt một số hình có tổng diện tích lớn hơn S thì có ít nhất hai trong số các hình đó có điểm chung.

Bài 1: Cho đa giác đều gồm 1999 cạnh. Người ta sơn các đỉnh của đa giác bằng 2 màu xanh và đỏ. Chứng minh rằng ắt phải tồn tại 3 đỉnh được sơn cùng một màu tạo thành một tam giác cân.

Hướng dẫn giải

Ta có đa giác 1999 cạnh nên có 1999 đỉnh. Do đó ắt phải tồn tại 2 đỉnh kề nhau là P và Q được sơn bởi cùng 1 màu (chẳng hạn màu đỏ).

Vì đa giác đã cho là đa giác đều có một số lẻ đỉnh, cho nên phải tồn tại một đỉnh nào đó nằm trên đường trung trực của đoạn thẳng PQ. Giả sử đỉnh đó là A .

Nếu A tô màu đỏ thì ta có ∆APQ là tam giác cân có 3 đỉnh A, P, Q được tô cùng màu đỏ.

Nếu A tô màu xanh. Lúc đó gọi B và C là các đỉnh khác của đa giác kề với P và Q.

Nếu cả 2 đỉnh B và C được tô màu xanh thì ∆ABC cân và có 3 đỉnh cùng tô màu xanh.

Nếu ngược lại một trong hai đỉnh B hoặc C mà tô màu đỏ thì tam giác BPQ hoặc tam giác CPQ là các tam giác cân có 3 đỉnh được tô màu đỏ.

Bài 2: Cho hình vuông ABCD và chín đường thẳng phân biệt thỏa mãn mỗi một đường thẳng đều chia hình vuông thành hai tứ giác có diện tích tỷ lệ với 2 và 3. Chứng minh rằng tồn tại ít nhất là ba đường thẳng đồng quy tại một điểm.

Hướng dẫn giải

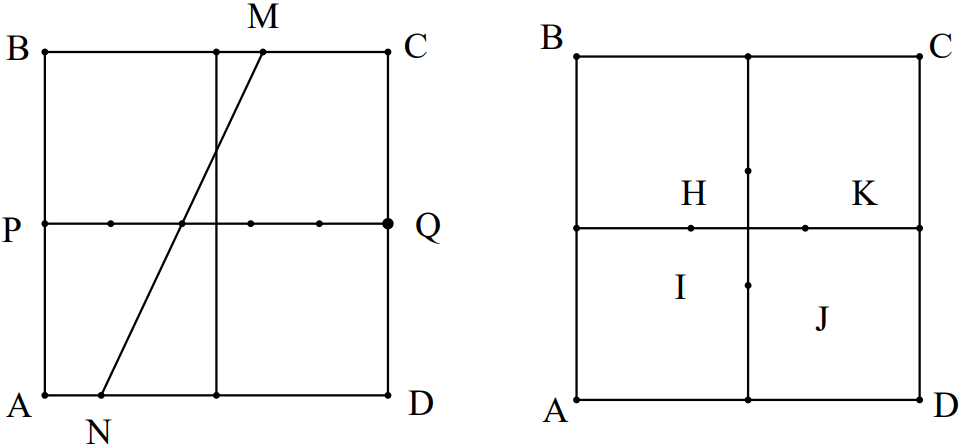
Nhận xét: Các đường thẳng đã cho không thể đi qua trung điểm các cạnh hình vuông ABCD bởi vì ngược lại thì hình vuông sẽ bị phân thành hai phần tam giác và ngũ giác.

Giả sử một đường thẳng trong số đó cắt cạnh BC tại M và cắt cạnh AD tại N.

Các hình thang ABMN và CDNM có chiều cao bằng nhau nên từ giả thiết suy ra MN chia đoạn thẳng nối trung điểm P, Q của AB và CD theo tỷ lệ 2/3.

Dễ thấy chỉ có 4 điểm chia 2 đường trung bình của hình vuông ABCD theo tỷ lệ 2/3 là I, J, K, H. Có 9 đường thẳng đia qua 4 điểm này; theo nguyên tắc Dirichlet, phải có ít nhất là 3 đường thẳng cùng đi qua một điểm.

3. Bài tập vận dụng về nguyên lý Dirichlet lớp 9

Bài 1: Một trường học có 10001000 học sinh gồm 2323 lớp. Chứng minh rằng phải có ít nhất một lớp có từ 4444 học sinh trở lên

Bài 2: Một lớp có 5050 học sinh. Chứng minh rằng có ít nhất 55 học sinh có tháng sinh giống nhau

Bài 3: Có năm loại học bổng khác nhau. Hỏi rằng phải có ít nhất bao nhiêu sinh viên để chắc chắn rằng có ít ra là 66 người cùng nhận học bổng như nhau.

Bài 4: Trong 4545 học sinh làm bài kiểm tra, không có ai bị điểm dưới 22, chỉ có 22 học sinh được điểm 1010. Chứng minh rằng ít nhất cũng tìm được 66 học sinh có điểm kiểm tra bằng nhau (điểm kiểm tra là một số tự nhiên)

Bài 5: Một lớp học có 5050 học sinh, có duy nhất một học sinh thiếu nhiều bài tập nhất là thiếu 33 bài tập. Chứng minh rằng tồn tại 1717 học sinh thiếu 11 số bài tập như nhau (trường hợp không thiếu bài tập coi như thiếu 0 bài)

Bài 6: Trong một phòng họp có n người, bao giờ cũng tìm được 2 người có số người quen trong số những người dự họp là như nhau.

Bài 7: Trong một lưới ô vuông kích thước 5 x 5, người ta điền ngẫu nhiên vào các ô một trong các giá trị -1, -0 hoặc 1, sau đó tính tổng tất cả các ô theo hàng, theo cột và theo hai đường chéo. Chứng minh rằng tồn tại ít nhất hai tổng có giá trị bằng nhau.

Bài 8: Giả sử trong một nhóm 6 người mỗi cặp hai hoặc là bạn hoặc là thù. Chứng tỏ rằng trong nhóm có ba người là bạn lẫn nhau hoặc có ba người là kẻ thù lẫn nhau.

Bài 9: Có 5 đấu thủ thi đấu cờ, mỗi người đấu một trận với mỗi đấu thủ khác. Chứng minh rằng trong suốt thời gian thi đấu, luôn tồn tại hai đấu thủ có số trận đã đấu bằng nhau.

Như vậy, bài viết trên đã giới thiệu đầy đủ kiến thức cần nhớ về nguyên lý Dirichlet lớp 9, cũng như cách làm các dạng bài về nguyên lý Dirichlet. Hy vọng các bạn ghi nhớ và áp dụng hiệu quả vào các bài toán cụ thể trong quá trình ôn thi vào 10.

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

[%Included.TAK12%]