Đề thi ĐGNL môn Toán vào lớp 10 mùa thi 2025
8/15/2024 9:05:00 AMĐề thi ĐGNL môn Toán vào lớp 10 mùa thi năm 2025 được biên soạn dựa theo cấu trúc đề thi chính thức của SGD Hà Nội và SGD TP.HCM các năm gần đây. Đề thi phủ kín 7/10 chủ điểm kiến thức và 20/28 dạng bài phổ biến nhất trong các đề thi tuyển sinh năm 2024, từ đó giúp HS xây dựng cho mình một lộ trình ôn tập hiệu quả.
- Số lượng câu hỏi: 20 câu
- Thời gian làm bài: 120 phút
Sau khi nộp bài, HS có thể xem giải thích đáp án chi tiết cho từng câu và báo cáo phân tích kết quả bài làm.
Cho △ ABC ᔕ △ MNP. Khi đó bằng
Cho đường thẳng (d): y = 2x + 1 và (d'): y = x + 10.
Tọa độ giao điểm A của đường thẳng (d) và (d') là
Cho biểu thức:
Thu gọn biểu thức đã cho ta được
Cho biểu thức:
Để biểu thức đã cho có nghĩa thì
Cho tam giác ABC có MN // BC. Biết AM = 4 cm, MB = 6 cm, BC = 15 cm như hình vẽ.
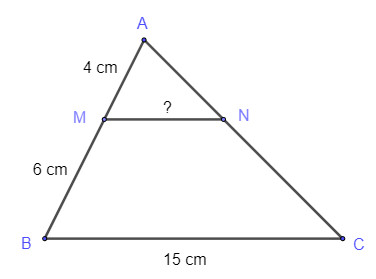
Khi đó MN bằng:
10 cm
2 cm
6 cm
9 cm
Cho đường thẳng (d): y = (m2 - 6m + 3)x + m và (d'): y = -5x + 2 với m là tham số.
Để (d) // (d') thì
m = 1 và m = 4
m = 2 và m = 4
m = 2
m = 4
Cho hệ phương trình
Hệ phương trình đã cho có nghiệm là
Cho phương trình:
Phương trình đã cho
- có 1 nghiệm
- có 2 nghiệm
- vô nghiệm
- có vô số nghiệm
Cho phương trình:
Phương trình đã cho có hai nghiệm là
x = 2 và x = 3
x = -2 và x = 3
x = 1 và x = -6
x = -1 và x = 6
Cho biểu thức:
Rút gọn biểu thức đã cho ta được
Cho bất phương trình:
Bất phương trình đã cho có nghiệm là
Cho tam giác ABC vuông tại A, đường cao AH (H ∈ BC), biết AC = 8 cm, số đo góc B bằng 60o.
Khi đó BH bằng:
Cho biểu thức
a) Rút gọn biểu thức A ta được
b) Có bao nhiêu giá trị nguyên dương của x để
Kết luận: Có giá trị nguyên dương của x thỏa mãn yêu cầu đề bài.
c) Có bao nhiêu giá trị nguyên của x để A nguyên.
Kết luận: Có giá trị nguyên của x để A nguyên.
Một người lái Cano từ địa điểm A đến địa điểm B trong một khoảng thời gian nhất định. Biết nếu người đó tăng tốc độ thêm 20 km/h thì người đó sẽ đến B sớm hơn dự kiến 1 giờ, nếu người đó giảm tốc độ đi 30 km/h thì người đó đến B muộn hơn dự kiến 3 giờ. Hỏi quãng đường AB dài bao nhiêu km?

Kết luận: Quãng đường AB dài km.
Cho tam giác ABC cân tại A, biết số đo góc A bằng 80o, AB = AC = 7 cm. Kẻ đường cao AD và BE cắt nhau tại H (D ∈ BC; E ∈ AC).
a) Độ dài cạnh BD là
b) Tính độ dài cạnh AH (*Lưu ý: Đáp án chỉ được làm tròn một lần duy nhất và làm tròn đến số thập phân thứ hai).
Kết luận: Độ dài cạnh AH bằng cm.
c) Qua A kẻ đường thẳng Ax song song với BC và cắt tia BE tại F.
Điền vào chỗ trống để hoàn thành phép chứng minh AE.AB = EF.BH
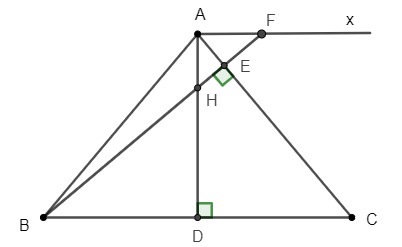
Ta có:
(Do )
Suy ra
Xét △ AHB và △ FBA có:
Góc ABF chung
Suy ra △ AHB ᔕ △ (g.g), ta được:
Ta có BC // AF nên:
Hay
Suy ra
Vì AC = nên hay
Từ (1) và (2) ta có
Suy ra AE.AB = EF. BH (đpcm)
Cho ba số thực a, b, c thỏa mãn a ≠ 0; b ≠ 0; c ≠ 0 và a.(a - b) + b.(b - c) = c.(a - c)
Tính giá trị của biểu thức:
Kết luận: B =