Hướng dẫn làm bài tập về số thập phân lớp 5

Bài tập về số thập phân lớp 5 là một trong những dạng bài quen thuộc trong chương trình toán lớp 5 và trong đề thi toán vào lớp 6. Để làm tốt bài tập này, học sinh cần nắm vững các khái niệm cơ bản như cấu tạo, cách đọc, viết, cũng như thực hiện các phép tính cộng, trừ, nhân, chia với số thập phân. Bài viết dưới đây sẽ tổng hợp các dạng bài tập về số thập phân lớp 5 thường gặp nhất, đi kèm với hướng dẫn giải chi tiết và bài tập áp dụng. Cùng theo dõi nhé!

1. Dạng 1: Đọc viết số thập phân

1.1. Kiến thức cần nhớ

Số thập phân gồm hai phần: phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.

• Những chữ số bên trái dấu phẩy thuộc về phần nguyên.
• Những chữ số bên phải dấu phẩy thuộc về phần thập phân.

Chú ý: Số tự nhiên có thể xem là số thập phân có phần thập phân chỉ gồm các chữ số 0. Ví dụ: số 57 có thể viết dưới dạng số thập phân: 57,0 hoặc 57,00...

[%Included.Dangky%]

1.2. Bài tập vận dụng

Ví dụ:

a) Số thập phân gồm sáu phần trăm, năm phần mười, bảy phần nghìn viết là?

b) Tìm một số thập phân bé nhất có 4 đơn vị, 3 phần mười, 5 phần nghìn.

Hướng dẫn giải

a) Số thập phân gồm sáu phần trăm, năm phần mười, bảy phần nghìn viết là: 0,567

Bài tập đọc và viết số thập phân

[%Included.Lớp 5%]

2. Dạng 2: So sánh số thập phân

2.1. Kiến thức cần nhớ

Để giải các bài toán so sánh số thập phân, ta thực hiện như sau:

• So sánh các phần nguyên của hai số đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.
• Nếu phần nguyên của hai số đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.
• Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.

2.2. Bài tập vận dụng

Ví dụ 1: Sắp xếp các số sau theo thứ tự từ lớn đến bé: 

6,375;                9,01;                  8,72;                 6,735;                  7,19

Hướng dẫn giải

So sánh phần nguyên: 9 > 8 > 7 > 6

So sánh phần thập phân với hai số 6,375 và 6,735 vì có cùng phần nguyên.

Ta có 3 phần mười nhỏ hơn 7 phần mười nên 6,375 < 6,735

Vậy: Các số được sắp xếp từ lớn đến bé là 9,01; 8,72; 7,19; 6,735; 6,375

Ví dụ 2: Trong các số 1,37; 1,62; 1,13; 1,94 thì số bé nhất là số nào?

Hướng dẫn giải

So sánh phần nguyên: 1 = 1 = 1 = 1

So sánh phần thập phân: 

Hàng phần mười: 1 < 3 < 6 < 9

Suy ra: 1,13 < 1,37 < 1,62 < 1,94

Vậy: Số bé nhất trong các số trên là số 1,13

Bài tập so sánh số thập phân

3. Dạng 3: Các phép tính với số thập phân

3.1. Kiến thức cần nhớ

Các phép tính với số thập phân	Luyện tập
Phép cộng hai số thập nhân Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau. Cộng như cộng các số tự nhiên. Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.	Phép cộng hai số thập nhân
Phép trừ hai số thập phân Ta viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau. Trừ như trừ các số tự nhiên. Đặt dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ	Phép trừ hai số thập phân
Phép nhân hai số thập nhân Nhân như nhân hai số tự nhiên. Đếm xem phần thập phân của các thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.	Phép nhân hai số thập nhân
Phép chia hai số thập phân Đếm xem có bao nhiêu chữ số ở phần thập phân (1 chữ số, 2 chữ số, 3 chữ số,…) của số chia thì ta nhân với số bị chia 10, 100, 1000,… Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia một số cho số tự nhiên.	Phép chia hai số thập phân

 

3.2. Bài tập vận dụng

Ví dụ 1: Tính 3,48 : 0,58 x 4,5 - 13,6 = ?

Hướng dẫn giải

3,48 : 0,58 x 4,5 - 13,6

= (3,48 : 0,58) x 4,5 - 13,6

= 6 x 4,5 - 13,6

= 27 - 13,6 = 13,4

Ví dụ 2: Tính (48 x 0,75 - 240 : 10) - (16 x 0,5 - 16 : 4) = ?

Hướng dẫn giải

(48 x 0,75 - 240 : 10) - (16 x 0,5 - 16 : 4)

= (36 - 24) - (8 - 4)

= 12 - 4 = 8

Bài tập các phép tính với số thập phân

4. Dạng 4: Cấu tạo số thập phân

4.1. Kiến thức cần nhớ

Phân tích cấu tạo số thập phân:

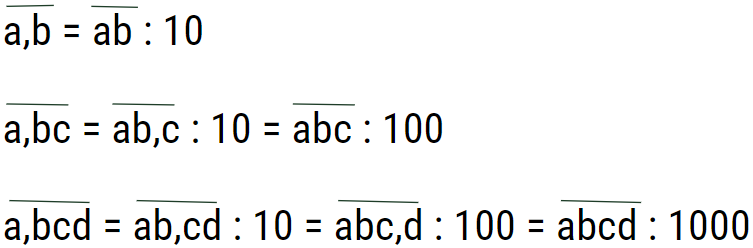
4.2. Bài tập vận dụng

Ví dụ 1: Tìm số thập phân biết a khác b và

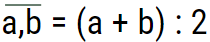
Hướng dẫn giải

Ví dụ 2: Khi cộng một số tự nhiên với một số thập phân, một bạn đã quên mất dấu phẩy ở số thập phân và đặt phép cộng như 2 số tự nhiên nên đã được tổng là 807. Hãy tìm số tự nhiên và số thập phân đó, biết tổng đúng của chúng là 241,71.

Hướng dẫn giải

Tổng của số tự nhiên và số thập phân là 241,71 nên số thập phân có 2 chữ số ở phần thập phân.

Nếu quên dấu phẩy ở số thập phân thì số đó tăng lên 100 lần. Tổng mới tăng lên 99 lần số thập phân.

Số thập phân là: (807 – 241,71) : 99 = 5,71

Số tự nhiên là: 241,71 – 5,71 = 236

Vậy: Hai số là 236 và 5,71

Bài tập cấu tạo số thập phân

5. Dạng 5: Tìm thành phần chưa biết của phép tính với số thập phân

5.1. Kiến thức cần nhớ

5.2. Bài tập vận dụng

Ví dụ 1: Tìm x, biết: (6,27 – 1,38) : (x : 2) = 3,26

Hướng dẫn giải

(6,27 – 1,38) : (x : 2) = 3,26

⇔ 4,89 : (x : 2) = 3,26

⇔ x : 2 = 4,89 : 3,26

⇔ x : 2 = 1,5

⇔ x = 1,5 x 2 = 3

Ví dụ 2: Tìm a, biết: (1,257 x a + 1,743 x a) - 2008 = 2009

Hướng dẫn giải

(1,257 x a + 1,743 x a) - 2008 = 2009

⇔ a x (1,257 + 1,743) = 2009 + 2008

⇔ 3 x a = 4017

⇔ a = 4017 : 3 = 1339

Bài tập tìm thành phần chưa biết của phép tính với số thập phân

6. Dạng 6: Các bài toán có lời văn với số thập phân

6.1. Kiến thức cần nhớ

6.2. Bài tập vận dụng

Ví dụ 1: Kho I có 361,5 tấn gạo và kho II có 226,5 tấn gạo. Sau khi người ta lấy ra ở mỗi kho một số tấn gạo như nhau thì còn lại số gạo ở kho II bằng số gạo kho I. Hỏi người ta đã lấy ra mỗi kho bao nhiêu tấn gạo?

Hướng dẫn giải

Khi lấy mỗi kho số tấn gạo bằng nhau thì hiệu số gạo giữa hai kho không thay đổi và bằng:

361,5 - 226,5 = 135 (tấn)

Sau khi lấy ra, số gạo còn lại ở kho II bằng ⅜ số gạo còn lại ở kho I. Theo đó, ta coi số gạo còn lại ở kho II là 3 phần thì số gạo còn lại ở kho I là 8 phần như thế.

Ta có sơ đồ sau:

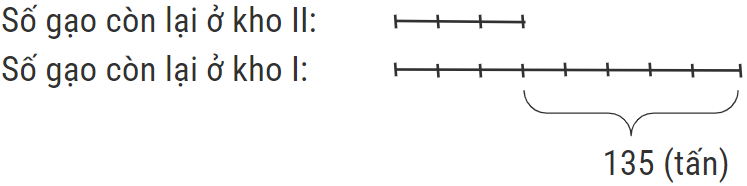
Từ sơ đồ ta thấy: 5 phần ứng với 135 tấn gạo.

Giá trị 1 phần là: 135 : 5 = 27 (tấn)

Số gạo còn lại ở kho II là: 27 x 3 = 81(tấn)

Số gạo lấy ở mỗi kho là: 

226,5 - 81 = 145,5 (tấn)

Vậy: Số gạo lấy ở mỗi kho là 145,5 tấn

Ví dụ 2: Kho I chứa 104,5 tấn ngô. Kho II chứa 75,5 tấn ngô. Người ta chuyển một số tấn ngô từ kho II sang kho I nên lượng ngô ở kho II bằng 2/7 lượng ngô ở kho I. Hỏi người ta đã chuyển từ kho II sang kho I bao nhiêu tấn ngô?

Hướng dẫn giải

Khi chuyển một số ngô từ kho II sang kho I thì tổng số ngô giữa hai kho không thay đổi và bằng:

104,5 + 75,5 = 180 (tấn)

Sau khi chuyển thì số ngô ở kho II bằng 2/7 số ngô ở kho I. Theo đó, ta coi số ngô sau khi chuyển ở khi II là 2 phần thì số ngô sau khi chuyển ở kho I là 7 phần như thế.

Ta có sơ đồ sau:

Từ sơ đồ ta thấy: 2 + 7 = 9 phần ứng với 180 tấn.

Giá trị 1 phần là: 180 : 9 = 20 (tấn)

Số ngô kho II sau khi chuyển là: 20 x 2 = 40 (tấn)

Số ngô chuyển từ kho II sang kho I là: 

75,5 - 40 = 35,5 (tấn)

Vậy: Số ngô chuyển từ kho II sang kho I là 35,5 tấn

Bài tập các bài toán có lời văn với số thập phân

Nội dung trên đã chia sẻ đến các em học sinh những dạng bài tập về số thập phân lớp 5 phổ biến nhất. Mong rằng những chia sẻ vừa rồi sẽ hữu ích cho các em học sinh trong quá trình học toán lớp 5 và ôn luyện vào lớp 6.

[%Included.TAK12%]