Hướng dẫn giải bài toán thực tế lớp 9
Bài toán thực tế lớp 9 là một trong những dạng bài tập thường gặp trong kỳ thi vào lớp 10. Để đồng hành cùng các em học sinh trong quá trình ôn thi toán vào 10, TAK12 sẽ chia sẻ phương pháp giải các bài toán thực tế có bài tập minh họa chi tiết, đi kèm là các bài tập vận dụng để học sinh ôn luyện. Cùng theo dõi nhé!
Nội dung bài viết:
1. Dạng 1: Các bài toán thực tế lớp 9 không lập phương trình hoặc hệ phương trình
1.1. Bài toán có mối quan hệ giữa các đại lượng biểu thị bằng bảng, biểu đồ
Phương pháp giải: Đọc, hiểu các thông số trong bảng để lập tỉ lệ để so sánh, thống kê giữa các đại lượng.
Bài tập minh họa
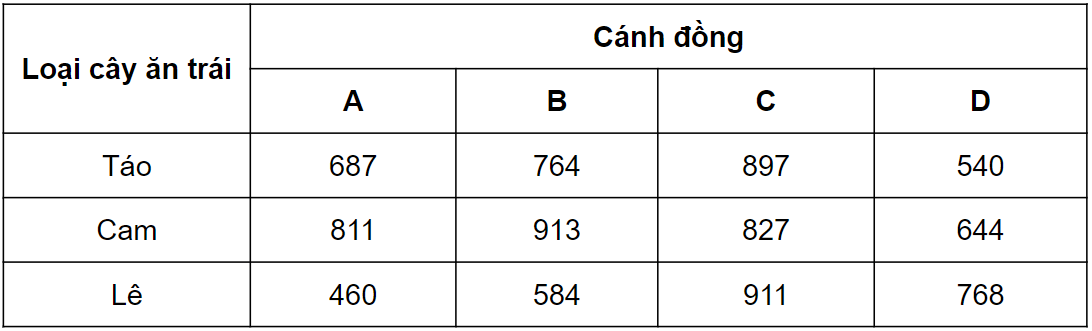
Bảng mô tả số cây ăn trái được trồng trên 5 cánh đồng. Nhìn vào bảng, em hãy trả lời câu hỏi sau:
a) Số cam cánh đồng A nhiều hơn số cam cánh đồng D là bao nhiêu cây?
b) Cánh đồng nào có ti lệ trồng lê cao nhất?
Hướng dẫn giải
a) Dựa vào bảng, ta có:
Số cam cánh đồng A nhiều hơn số cam cánh đồng D là : 811 - 644 = 167 cây
b) Dựa vào bảng, ta có:
+ Tỉ lệ trồng lê ở cánh đồng A là: 460 : (687 + 811 + 460) = 0,37459 ≈ 0,37
+ Tỉ lệ trồng lê ở cánh đồng B là: 584 : (764 + 913 + 584) = 0,25829 ≈ 0,26
+ Tỉ lệ trồng lê ở cánh đồng C là: 911 : (897 + 827 + 911) = 0,345 ≈ 0,35
+ Tỉ lệ trồng lê ở cánh đồng D là: 678 : (540 + 644 + 678) = 0,3641 ≈ 0,36
Vậy tỉ lệ trồng lê ở cánh đồng A là cao nhất
[%Included.Lớp 9%]
Bài tập vận dụng
Theo quyết định của Bộ Công Thương ban hành, giá bán lẻ điện sinh hoạt từ ngày 16/03 sẽ dao động trong khoảng từ 1484 đến 2587 đồng mỗi kWh tùy bậc thang. Dưới đây là bảng so sánh biểu giá điện trước và sau khi điều chỉnh:
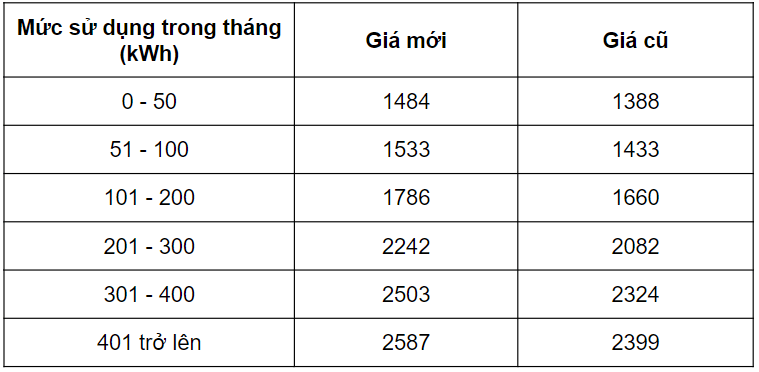
a) Biết trong tháng 1 hộ A tiêu thụ 140 kWh thì hộ A phải trả bao nhiêu tiền?
b) Nếu hộ A trung bình mỗi tháng tiêu thụ 140 kWh thì theo giá mới số tiền phải trả tăng lên bao nhiêu trong 1 tháng?
[%Included.Dangky%]
1.2. Bài toán về ứng dụng hình học
Phương pháp giải: Hiểu tình huống đề bài đưa ra, sau đó vẽ hình minh họa và vận dụng kiến thức hình học để giải bài toán.
Bài tập minh họa
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Gần đấy có một toà nhà cao tầng có bóng trên mặt đất là 80m (như hình vẽ). Em hãy cho biết toà nhà có bao nhiêu tầng, biết rằng mỗi tầng cao 3,5 m.
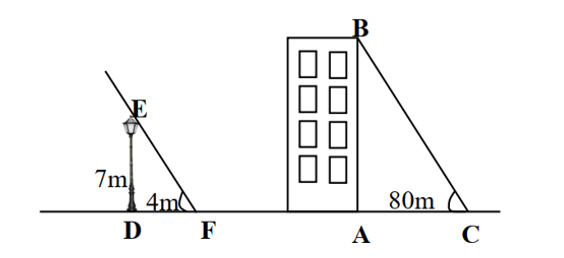
Hướng dẫn giải
Xét ∆ABC và ∆DEF ta có:
Góc EDF = góc BAC = 90°
Góc EFD = góc BCA (gt)
Do đó, ∆ABC ∾ ∆DEF (g.g)
⇒ AB/DE = AC/DF
⇒ AB/7 = 80/4
⇒ AB = 140 (m)
Toà nhà cao 140 m.
Số tầng của toà nhà là: 140 : 3,5 = 40 (tầng).
Bài tập vận dụng
Bài 1: Khi uống nước giải khát, người ta hay sử dụng ống hút nhựa dạng hình trụ đường kính đáy là 0,4cm, chiều dài ống hút là 18cm. Hòi khi thải ra môi trường, diện tích nhựa gây ô nhiễm cho môi trường do 100 ống hút này gây ra là bao nhiêu?
Bài 2: Ngày 4 - 6 - 1783, anh em nhà Mông-gôn-fi-ê (người Pháp) phát minh ra khinh khí cầu dùng không khí nóng. Coi khinh khí cầu này là hình cầu có đường kính 11m và được làm bằng vải dù. Hãy tính diện tích vải dù để làm khinh khí cầu đó (lấy π = 3,14 và làm tròn kết quả đến chữ số thập phần thứ hai).
Bài 3: Người ta cho một quả trứng vào cốc thủy tinh có nước, hình trụ; thấy trứng chìm hoàn toàn xuống dưới đáy và nằm ngang thì chứng tỏ quả trứng đó còn tươi. Em hãy tính thể tích quả trứng đó, biết diện tích đáy của cột nước hình trụ là 16,7cm2 và nước trong lọ dâng lên thêm 8,2mm khi quả trứng chìm hoàn toàn trong nước.
👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9
1.3. Bài toán dùng sơ đồ Ven
Phương pháp giải: Dùng biểu đồ Ven đề mô tả mối quan hệ giữa các đại lượng trong bài toán. Từ biểu đồ, học sinh sẽ suy luận và tính các đại lượng bài toán yêu cầu.
Bài tập minh họa
Lớp 9A có 30 học sinh đạt loại giỏi ít nhất một trong 2 môn Văn và Toán, trong đó có 18 em đạt giỏi môn Văn, 24 em đạt giỏi môn Toán. Hỏi có bao nhiêu em giỏi cả 2 môn Văn và Toán.
Hướng dẫn giải
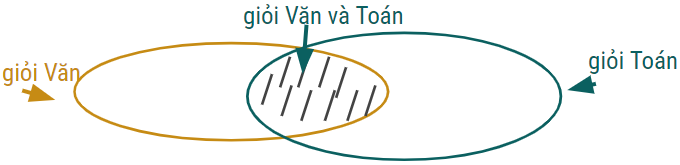
Số học sinh chỉ giỏi Văn là: 30 - 24 = 6 (học sinh)
Số học sinh giỏi cả Văn và Toán là: 18 - 6 = 12 (học sinh)
Vậy số học sinh giỏi cả Văn và Toán là 12 học sinh.
Bài tập vận dụng
Bài 1: Đội tuyển thi đá cầu và đấu cờ vua của Trường Tiểu học Võ Thị Sáu có 22 em, trong đó có 15 em thi đá cầu và 12 em thi đấu cờ vua. Hỏi có bao nhiêu em trong đội tuyển thi đấu cả hai môn?
Bài 2: Trong một hội nghị có 100 đại biểu tham dự. Mỗi đại biểu nói được một hoặc hai hoặc ba thứ tiếng: Nga, Anh hoặc Pháp. Biết rằng có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu nói được tiếng Pháp, 8 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi có bao nhiêu đại biểu chỉ nói được tiếng Nga?
Bài 3: Trường Ban Mai có 40 em học sinh dự thi ba môn: nhảy dây, chạy và đá cầu. Trong đó có 8 em chỉ thi nhảy dây, 20 em thi chạy và 18 em thi đá câù. Hỏi có bao nhiêu em vừa thi chạy vừa thi đá cầu?
2. Dạng 2: Các bài toán thực tế lớp 9 lập phương trình hoặc hệ phương trình
Phương pháp chung để giải bài toán thực tế lớp 9 bằng cách lập phương trình hoặc hệ phương trình:
Bước 1: Lập phương trình hoặc hệ phương trình
- Đặt ẩn và xác định điều kiện, đơn vị cho ẩn.
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Lập phương trình hoặc hệ phương trình liên hệ giữa các đại lượng.
Bước 2: Giải phương trình hoặc hệ phương trình, đối chiếu nghiệm với điều kiện.
Bước 3: Kết luận
2.1. Bài toán dạng chuyển động

Bài tập minh họa
Một người đi xe máy từ A đến B với vận tốc 30 km/h, rồi từ B về A với vận tốc 50 km/h. Tổng thời gian cả đi cả về là 5 giờ 20 phút. Tính quãng đường AB.
Hướng dẫn giải
Gọi chiều dài quãng đường AB là: x (x > 0, km)
Thời gian xe đi từ A đến B là: x/30 (h)
Thời gian xe đi từ B về A là: x/50 (h)
Vì tổng thời gian cả đi và về bằng 5 giờ 20 phút = 16/3 giờ nên ta có phương trình:
x/30 + x/50 = 16/3
⇔ 5x + 3x = 800
⇔ 8x = 800
⇔ x = 100 (thỏa mãn)
Vậy: Quãng đường AB dài 100km.
Bài toán thực tế lớp 9 dạng chuyển động
2.2. Bài toán về tỉ số phần trăm, lãi suất

Bài tập minh họa
Ví dụ 1: Dân số hiện nay của một phường là 40000 người. Sau 2 năm dân số của phường được dự tính là 41618 người. Hỏi mỗi năm dân số của phường tăng bao nhiêu phần trăm?
Hướng dẫn giải
Gọi tỉ lệ tăng dân số của phương là x(%) (x > 0)
Sau 1 năm dân số của phường tăng lên là: 40000x (người)
Số dân của phường sau 1 năm là: 40000 + 40000x (người)
Sau 2 năm dân số của phường tăng lên là :( 40000 + 40000x)x (người)
Mặt khác theo đề bài sau 2 năm dân số của phường tăng lên: 41618 – 40000 = 1618 (người)
Từ đó ta có phương trình:
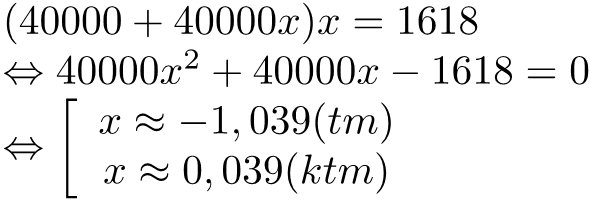
Vậy tỉ lệ tăng dân số là 3,9%
Ví dụ 2: Ông Bình gửi một số tiền vào ngân hàng, sau 8 tháng ông có việc cần tiền, nên phải rút số tiền đó ra với lãi suất 3% mỗi năm. Tính số tiền ông Bình gửi vào ngân hàng, biết số tiền cả vốn lẫn lãi mà ông nhận được là 153 000 000 đồng.
Hướng dẫn giải
Gọi số tiền ông Bình gửi vào ngân hàng là x (x > 0, đồng)
Lãi suất 1 tháng là: 3% : 12 = 0,25%
Số tiền lãi 8 tháng ông nhận được sau khi rút tiền là:
8.0,25%x = 2%x = 0,02x (đồng)
Tổng số tiền ông Bình nhận được (cả gốc và lãi) là:
x + 0,02x (đồng)
Vì số tiền ông Bình nhận được là 153 000 000 đồng nên ta có phương trình:
x + 0,02x = 153 000 000
1,02x = 153 000 000
x = 150 000 000 (thỏa mãn)
Vậy: Số tiền ông Bình gửi là 150 000 000 đồng.
Bài toán thực tế lớp 9 về tỉ số phần trăm, lãi suất
2.3. Bài toán về giá cước Taxi
Phương pháp giải: Mỗi bài toán về giá cước taxi sẽ có cách tính tiền khác nhau. Để giải bài toán, ta cần phân tích đề bài để biết cách tính tiền trong từng trường hợp.
Bài tập minh họa
Bảng giá cước của một công ty taxi A được cho như bảng sau:
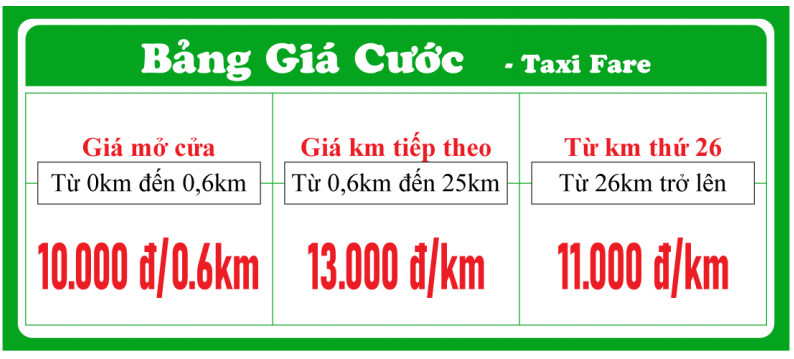
Một hành khách thuê taxi đi quãng đường 30km phải trả số tiền là bao nhiêu?
Hướng dẫn giải
Gọi y là số tiền phải trả; x là số km phải đi
Ta có:
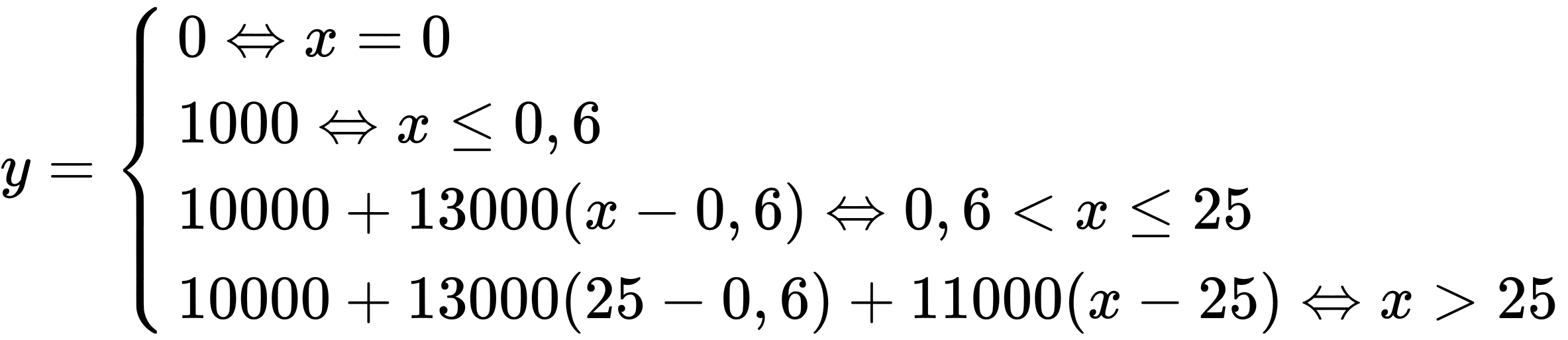
Với x = 30 > 25 ⇒ y = 10000 + 13000(25 − 0,6) + 11000(30 − 25) = 382200đ
Vậy hành khách thuê taxi đi quãng đường 30km phải trả số tiền là 382200đ
Bài tập vận dụng
Bảng giá cước của một hãng Taxi được cho như sau:

Một hành khách thuê taxi đi quãng đường 35km phải trả số tiền là bao nhiêu?
2.4. Bài toán sử dụng các kiến thức vật lý, hóa học
Phương pháp giải: Sử dụng công thức toán học, vật lý hoặc hóa học để giải bài toán.
Bài tập minh họa
Bạn An muốn có 1 lít nước ở nhiệt độ 35°C. Hỏi bạn cần phải đổ bao nhiêu lít nước đang sôi vào bao nhiêu lít nước ở nhiệt độ 15°C. Lấy nhiệt dung riêng của nước là 4190 J/kgK?
Hướng dẫn giải
Gọi x là khối lượng nước ở 15°C và y là khối lượng nước đang sôi (x,y > 0, lít)
Ta có: x + y = 1
Nhiệt lượng y kg nước đang sôi tỏa ra: Q1 = y. 4190(100 – 35)
Nhiệt lượng x kg nước ở nhiệt độ 15°C thu vào để nóng lên 35°C: Q2 = x.4190(35 – 15)
Nhiệt lượng tỏa ra bằng nhiệt lượng thu vào:
Q1 = Q2
⇔ x.4190(35 - 15) = y.4190(100 - 35)
⇔ 20x = 65y
⇔ 4y = 13y
Ta có hệ phương trình:
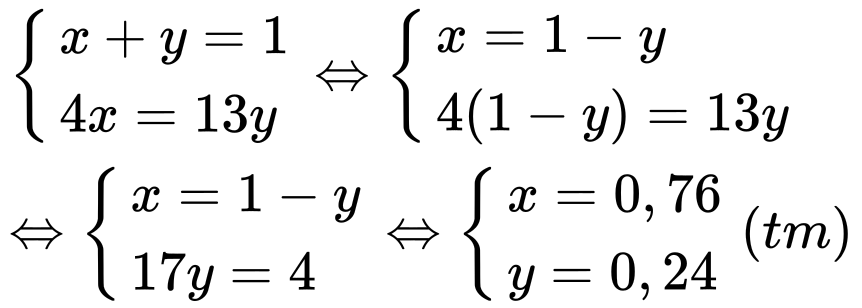
Vậy Bạn An cần phải đổ 0,24 lít nước đang sôi vào 0,76 lít nước ở 15°C để được 1lít nước ở nhiệt độ 35°C.
Bài tập vận dụng
Bài 1: Pha 2 lít nước sôi (1000C) và 3 lít nước lạnh (200C) thì được hỗn hợp nước có nhiệt độ bao nhiêu?
Bài 2: Khi thêm 200g axit vào dung dịch A được dung dịch B có nồng độ axit là 50%. Lại thêm 300g nước vào dung dịch B được dung dịch C có nồng độ axit là 40%. Tính nồng độ axit trong dung dịch A.
Bài 3: Có hai loại quặng chứa 75% sắt và 50% sắt. Tính khối lượng của mỗi loại quặng đem trộn để được 25 tấn quặng sắt chứa 66% sắt.
2.5. Bài toán về tuổi
Lưu ý khi giải bài toán về tuổi: Cứ mỗi năm người này tăng một tuổi thì người kia cũng tăng một tuổi nên hiệu số tuổi của hai người không thay đổi theo thời gian.
Bài tập minh họa
Năm nay tuổi mẹ gấp 7 lần tuổi con. 8 năm sau, tuổi mẹ gấp 3 lần tuổi con. Tính tuổi của mỗi người hiện nay.
Hướng dẫn giải
Gọi tuổi con và tuổi mẹ hiện nay lần lượt là x, y
(x, y ∈ N*, x < y, tuổi)
Vì hiện nay tuổi mẹ gấp 7 lần tuổi con nên ta có phương trình
7 x = y = 7x - y = 0 (1)
8 năm sau tuổi của con là: x + 8 (tuổi)
8 năm sau tuổi của mẹ là: y + 8 (tuổi)
Vì 8 năm sau tuổi mẹ gấp 3 lần tuổi con, nên ta có phương trình 3(x + 8) = y + 8
⇔ 3x + 24 = y + 8 ⇔ 3x - y = -16 (2)
Từ (1) và (2) ta có hệ phương trình:
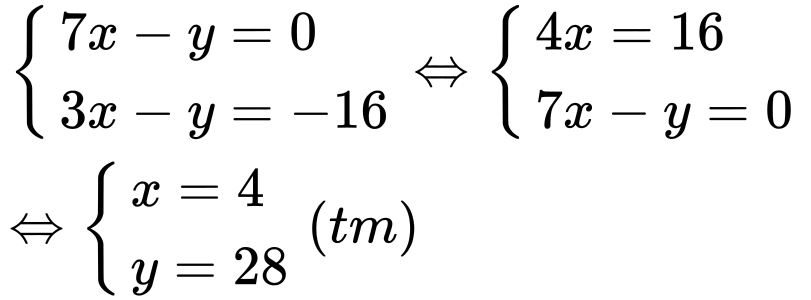
Vậy năm nay tuổi con là 4 tuổi, tuổi mẹ là 28 tuổi.
Bài toán thực tế lớp 9 về tuổi
2.6. Bài toán về năng suất

Bài tập minh họa
Một phân xưởng theo kế hoạch cần phải sản xuất 1200 sản phẩm trong một số ngày quy định. Khi thực hiện, do mỗi ngày phân xưởng đó sản xuất vượt mức 10 sản phẩm nên phân xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định 4 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng đó cần sản xuất bao nhiêu sản phẩm?
Hướng dẫn giải
Gọi số sản phẩm mỗi ngày phân xưởng đó làm được theo kế hoạch là x (x ∈ N*; sp)
Thời gian hoàn thành 1200 sản phẩm theo kế hoạch là 1200/x (ngày)
Thực tế, mỗi ngày xưởng đó làm được x + 10 (sp)
Thời gian thực tế hoàn thành 1200 sản phẩm là 1200/(x+10) (ngày)
Vì xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định 4 ngày, nên ta có phương trình:
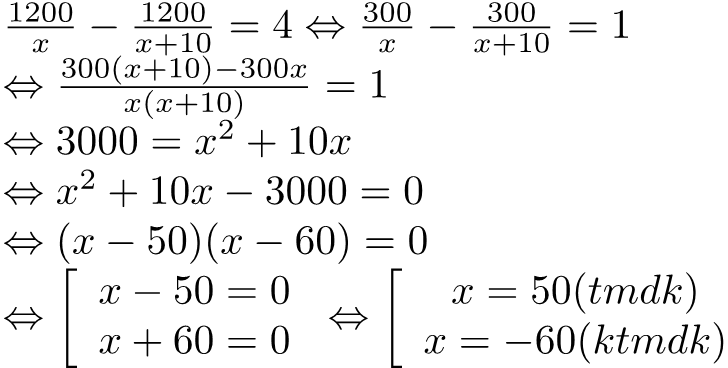
Vậy theo kế hoạch, mỗi ngày phân xưởng đó phải làm 50 sản phẩm.
Bài toán thực tế lớp 9 về năng suất
2.7. Bài toán hình học (chu vi, diện tích, thể tích)
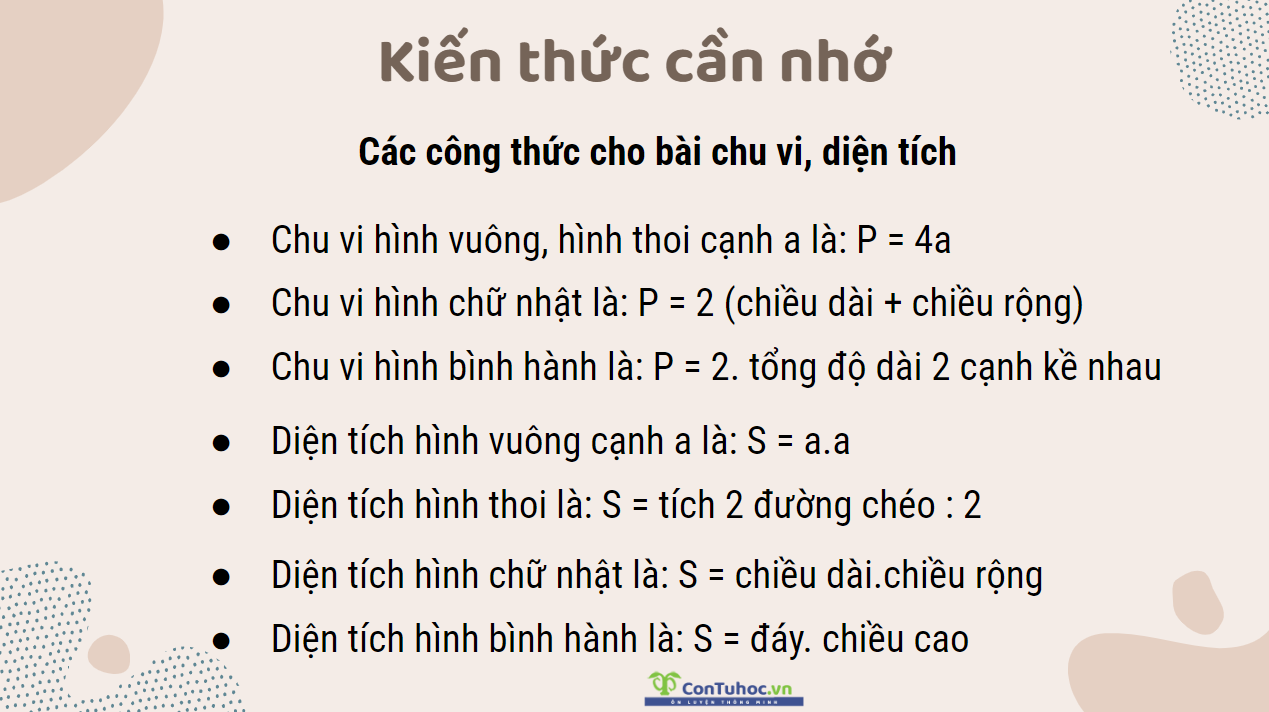

Bài tập minh họa
Chu vi một khu vườn hình chữ nhật bằng 60m, hiệu độ dài của chiều dài và chiều rộng là 20m. Tìm độ dài các cạnh của hình chữ nhật.
Hướng dẫn giải
Gọi chiều dài của khu vườn là x (m) (20 < x < 30)
Chiều rộng của khu vườn là x – 20 (m)
Chu vi của khu vườn bằng 60m nên ta có phương trình:
(x + x – 20).2 = 60 ⇔ 2x – 20 = 30 ⇔ 2x = 50 ⇔ x = 25 (thỏa mãn)
Vậy: Chiều dài của mảnh vườn là 25m, chiều rộng là 25 - 20 = 5m.
Bài toán thực tế lớp 9 về hình học (chu vi, diện tích, thể tích)
Nội dung vừa rồi đã chia sẻ hướng dẫn giải bài toán thực tế lớp 9 chi tiết đến các em học sinh. Mong rằng những thông tin trên sẽ giúp ích các em trong quá trình chuẩn bị ôn luyện toán lớp 9 và thi vào 10.
[%Included.TAK12%]