Hướng dẫn giải bài toán bằng cách lập phương trình lớp 9

Giải bài toán bằng cách lập phương trình lớp 9 là một trong những dạng bài tập thường gặp khi ôn luyện vào lớp 10. Để đồng hành cùng các em học sinh trong quá trình ôn thi toán vào 10, TAK12 sẽ chia sẻ phương pháp chung để giải bài toán bằng cách lập phương trình lớp 9, đồng thời hướng dẫn chi tiết cách giải từng dạng bài tập cụ thể trong chủ đề này. Cùng theo dõi nhé!

1. Phương pháp chung để giải bài toán bằng cách lập phương trình lớp 9

Các bước để giải bài toán bằng cách lập phương trình lớp 9:

Bước 1: Lập phương trình

• • Đặt ẩn và xác định điều kiện, đơn vị cho ẩn. 
  • Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết. 
  • Lập phương trình liên hệ giữa các đại lượng.

Bước 2: Giải phương trình, đối chiếu nghiệm với điều kiện.

Bước 3: Kết luận

👉 Luyện tập Giải bài toán bằng cách lập hệ phương trình

[%Included.Lớp 9%]

2. Hướng dẫn giải dạng bài toán bằng cách lập phương trình lớp 9

2.1. Dạng 1: Giải bài toán tỉ lệ phần trăm, lãi suất ngân hàng bằng cách lập phương trình

Bài tập minh họa

Ông Bình gửi một số tiền vào ngân hàng, sau 8 tháng ông có việc cần tiền, nên phải rút số tiền đó ra với lãi suất 3% mỗi năm. Tính số tiền ông Bình gửi vào ngân hàng, biết số tiền cả vốn lẫn lãi mà ông nhận được là 153 000 000 đồng.

Hướng dẫn giải

Gọi số tiền ông Bình gửi vào ngân hàng là x (x > 0, đồng)

Lãi suất 1 tháng là: 3% : 12 = 0,25%

Số tiền lãi 8 tháng ông nhận được sau khi rút tiền là:

8.0,25%x = 2%x = 0,02x (đồng)

Tổng số tiền ông Bình nhận được (cả gốc và lãi) là:

x + 0,02x (đồng)

Vì số tiền ông Bình nhận được là 153 000 000 đồng nên ta có phương trình:

x + 0,02x = 153 000 000

1,02x = 153 000 000

x = 150 000 000 (thỏa mãn)

Vậy: Số tiền ông Bình gửi là 150 000 000 đồng.

[%Included.Dangky%]

Bài tập áp dụng

👉 Thực hành các bài tập giải bài toán tỉ lệ phần trăm, lãi suất ngân hàng bằng cách lập phương trình

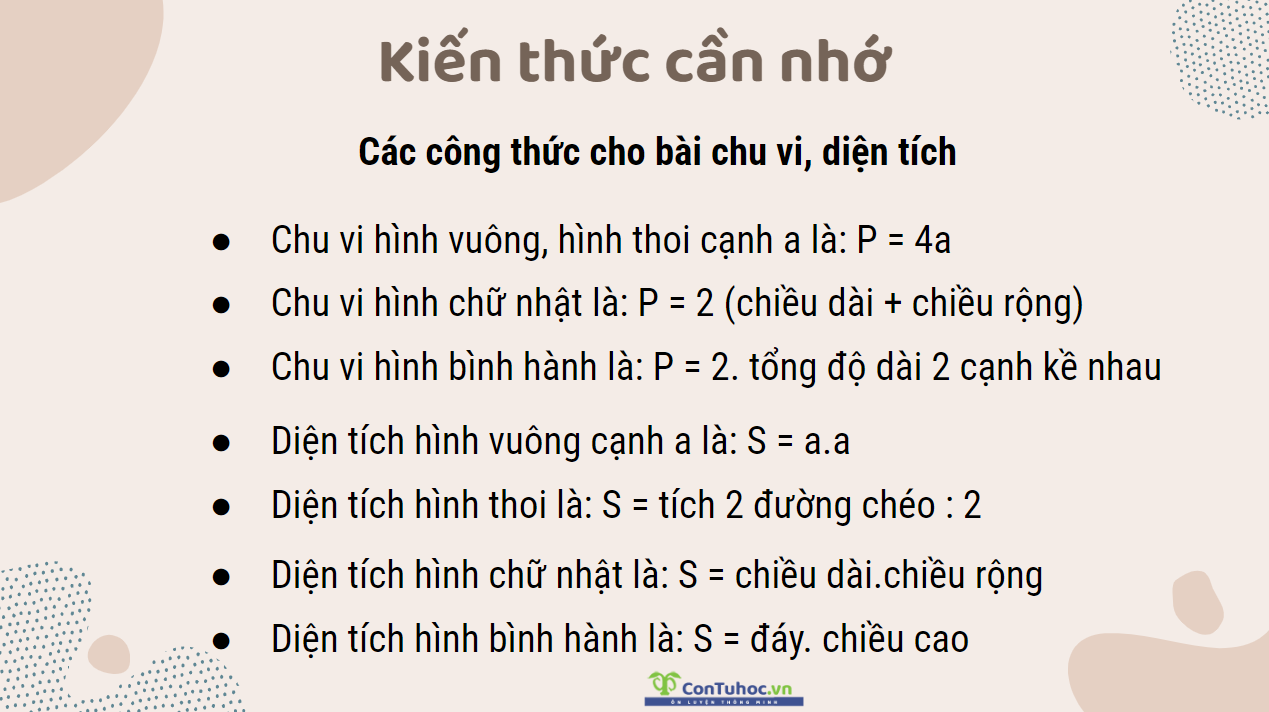
2.2. Dạng 2: Giải bài toán hình học (chu vi, diện tích, thể tích) bằng cách lập phương trình

 

Bài tập minh họa

Chu vi một khu vườn hình chữ nhật bằng 60m, hiệu độ dài của chiều dài và chiều rộng là 20m. Tìm độ dài các cạnh của hình chữ nhật.

Hướng dẫn giải

Gọi chiều dài của khu vườn là x (m) (20 < x < 30)

Chiều rộng của khu vườn là x – 20 (m)

Chu vi của khu vườn bằng 60m nên ta có phương trình:

(x + x – 20).2 = 60 ⇔ 2x – 20 = 30 ⇔ 2x = 50 ⇔ x = 25 (thỏa mãn)

Vậy: Chiều dài của mảnh vườn là 25m, chiều rộng là 25 - 20 = 5m.

Bài tập áp dụng

👉 Thực hành các bài tập giải bài toán hình học (chu vi, diện tích, thể tích) bằng cách lập phương trình

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

2.3. Dạng 3: Giải bài toán chuyển động bằng cách lập phương trình

Bài tập minh họa

Một người đi xe máy từ A đến B với vận tốc 30 km/h, rồi từ B về A với vận tốc 50 km/h. Tổng thời gian cả đi cả về là 5 giờ 20 phút. Tính quãng đường AB.

Hướng dẫn giải

Gọi chiều dài quãng đường AB là: x (x > 0, km)

Thời gian xe đi từ A đến B là:

Thời gian xe đi từ B về A là:

Vì tổng thời gian cả đi và về bằng nên ta có phương trình:

⇔ 5x + 3x = 800

⇔ 8x = 800

⇔ x = 100 (thỏa mãn)

Vậy: Quãng đường AB dài 100km.

Bài tập áp dụng

👉 Thực hành các bài tập giải bài toán chuyển động bằng cách lập phương trình

2.4. Dạng 4: Giải bài toán năng suất bằng cách lập phương trình

Bài tập minh họa

Một phân xưởng theo kế hoạch cần phải sản xuất 1200 sản phẩm trong một số ngày quy định. Khi thực hiện, do mỗi ngày phân xưởng đó sản xuất vượt mức 10 sản phẩm nên phân xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định 4 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng đó cần sản xuất bao nhiêu sản phẩm?

Hướng dẫn giải

Gọi số sản phẩm mỗi ngày phân xưởng đó làm được theo kế hoạch là x (x ∈ N*; sp) 

Thời gian hoàn thành 1200 sản phẩm theo kế hoạch là (ngày)

Thực tế, mỗi ngày xưởng đó làm được x + 10 (sp)

Thời gian thực tế hoàn thành 1200 sản phẩm là (ngày)

Vì xưởng đã hoàn thành kế hoạch sớm hơn thời gian quy định 4 ngày, nên ta có phương trình:

⇔ 3000 = x² + 10x

⇔ x² + 10x - 3000 = 0

⇔ (x - 50)(x - 60) = 0

 

Vậy: Theo kế hoạch, mỗi ngày phân xưởng đó phải làm 50 sản phẩm.

Bài tập áp dụng

👉 Thực hành các bài tập giải bài toán năng suất bằng cách lập phương trình

2.5. Dạng 5: Giải bài toán về tuổi bằng cách lập phương trình

Bài tập minh họa

Mẹ hơn con 24 tuổi. Sau 2 năm nữa thì tuổi mẹ gấp 3 lần tuổi con. Tuổi của con hiện nay là bao nhiêu?

Hướng dẫn giải

Gọi số tuổi của con hiện tại là x (tuổi)

Số tuổi của mẹ là x + 24 (tuổi)

Ta có: 3(x + 2) = x + 24 + 2

⇒ x = 10 

Vậy: Hiện tại tuổi của con là 10 tuổi.

Bài tập áp dụng

👉 Thực hành các bài tập giải bài toán về tuổi bằng cách lập phương trình

2.6. Dạng 6: Giải bài toán về cấu tạo số nguyên bằng cách lập phương trình

Bài tập minh họa

Tìm một số có hai chữ số, biết rằng chữ số hàng đơn vị bé ơn chữ số hàng chục là 2, tổng các bình phương của hai chữ số bé hơn số đã cho là 19.

Hướng dẫn giải

Gọi chữ số hàng đơn vị là x (x ∈ N*, x ≤ 9)

Khi đó chữ số hàng chục là x + 2.

Tổng các bình phương của hai chữ số là (x + 2)² + x2

Số đã cho là 10(x + 2) + x.

Theo đầu bài ra ta có phương trình (x + 2)² + x² + 19 = 10(x + 2) + x

⇔ 2x² - 7x + 3 = 0

⇔

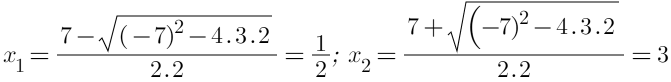
Vì x phải là số nguyên nên chữ số hàng đơn vị là 3.

Vậy: Số phải tìm là 53.

Bài tập áp dụng

👉 Thực hành các bài tập giải bài toán về cấu tạo số nguyên bằng cách lập phương trình

Nội dung vừa rồi đã chia sẻ hướng dẫn giải bài toán bằng cách lập phương trình lớp 9 chi tiết đến các em học sinh. Mong rằng những thông tin trên sẽ giúp ích các em trong quá trình học môn Toán lớp 9.

[%Included.TAK12%]