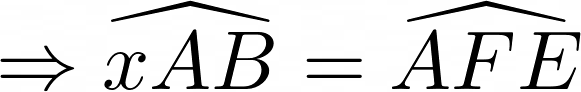Hướng dẫn làm bài tập đường tròn lớp 9

Đường tròn là chủ điểm kiến thức hình học đặc biệt quan trọng với học sinh lớp 9 ôn thi vào 10. Trong nội dung sau đây, TAK12 sẽ cung cấp cho học sinh những kiến thức cơ bản về đường tròn, đồng thời hướng dẫn các em làm tốt các bài tập đường tròn lớp 9.

1. Kiến thức cần nhớ về đường tròn lớp 9

Nhằm hỗ trợ các em học sinh lớp 9 tổng hợp kiến thức cần nhớ về đường tròn để ôn toán vào 10, TAK12 đã hệ thống kiến thức về đường tròn lớp 9 học kì 1 và học kì 2 (bộ sách Kết nối) trong bảng dưới đây. Với mỗi bài học, TAK12 đã biên soạn slide bài giảng chi tiết, đi kèm là các bài tập vận dụng lý thuyết có hướng dẫn giải để học sinh ôn luyện.

Học kì	Bài học về Đường tròn
Học kì 1	Mở đầu về đường tròn Cung và dây của một đường tròn Độ dài cung tròn. Diện tích hình quạt tròn và hình vành khuyên   Vị trí tương đối của đường thẳng và đường tròn Vị trí tương đối của hai đường tròn
Học kì 2	Góc nội tiếp Đường tròn ngoại tiếp và đường tròn nội tiếp Tứ giác nội tiếp Đa giác đều

[%Included.Dangky%]

[%Included.Lớp 9%]

2. Tổng hợp bài tập đường tròn lớp 9 học kì 1

2.1. Bài toán mở đầu về đường tròn

Bài toán: Gọi O là trung điểm của đoạn thẳng AB. Chứng minh rằng đường tròn (O; OA) đi qua B.

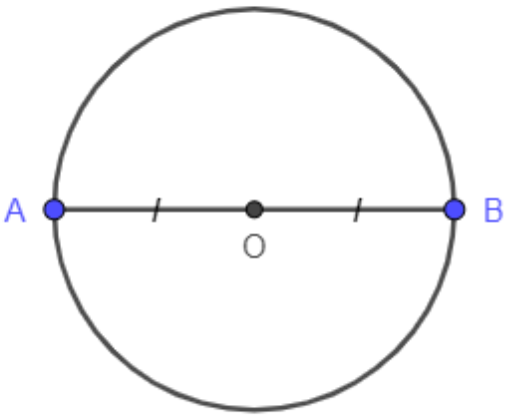
Hướng dẫn giải

Vì O là trung điểm của đoạn AB nên OB = OA.

Do đó B (O; OA), nói cách khác, đường tròn (O; OA) đi qua B.

👉 Luyện chủ điểm: Mở đầu về đường tròn

2.2. Bài toán cung và dây của một đường tròn

Bài toán 1: Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) nằm trên đường tròn, ta đều có BC < AB + AC < 2BC

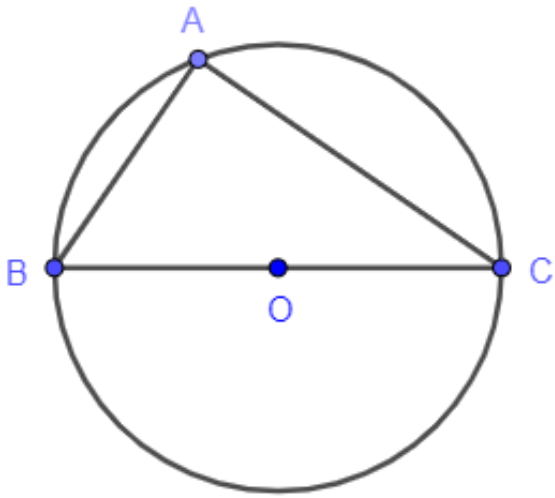
Hướng dẫn giải

Xét tam giác ABC có: BC < AB + AC (1)

Xét đường tròn đường kính BC có dây cung AB, AC nên:

AB < BC; AC < BC

Suy ra: AB + AC < 2BC (2)

Từ (1) và (2) suy ra: BC < AB + AC < 2BC (đpcm)

Bài toán 2: Cho ba điểm A, B và C thuộc (O) như hình vẽ.

a) Tìm các góc ở tâm có hai cạnh đi qua hai trong ba điểm A, B, C.

b) Tìm các cung có hai mút là hai trong ba điểm A, B, C.

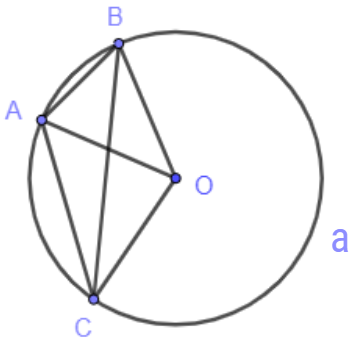
Hướng dẫn giải

a) Tìm các góc ở tâm có hai cạnh đi qua hai trong ba điểm A, B, C

Các góc ở tâm cần tìm là góc AOB, góc BOC, góc COA

b) Tìm các cung có hai mút là hai trong ba điểm A, B, C

Các cung có hai mút A, B là cung AB, cung ACB.

Các cung có hai mút A, C là cung AC, cung ABC.

Các cung có hai mút B, C là cung BAC, cung BaC.

👉 Luyện chủ điểm: Cung và dây của một đường tròn

👉 Gợi ý các phần mềm học tập và ôn thi hiệu quả cho học sinh lớp 9

2.3. Bài toán độ dài cung tròn, diện tích hình quạt tròn và hình vành khuyên

Bài toán 1: Cho hai điểm A và B là hai điểm trên đường tròn (O; 6 cm) sao cho góc AOB = 60°. Tính số đo và độ dài cung nhỏ AB.

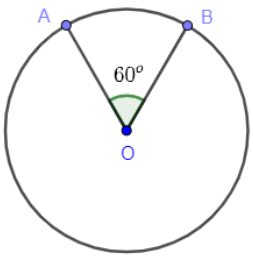
Hướng dẫn giải

Ta có: số đo cung AB = góc AOB = 60°

Độ dài l của cung nhỏ AB là:

l = 60/180.π.6 = 2π (cm)

Bài toán 2: Tính diện tích hình quạt tròn bán kính 6 cm và có độ dài cung tương ứng với nó bằng 5π cm.

Hướng dẫn giải

Hình quạt tròn có độ dài cung tương ứng với nó là l = 5π cm, bán kính là R = 6 cm.

Do đó diện tích S của hình quạt tròn là:

S = l.R.½ = 5π.6.½ = 15π (cm²)

Bài toán 3: Tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 5 m và 6 m.

Hướng dẫn giải

Gọi S_v là diện tích hình vành khuyên cần tính, khi đó:

S_v = π(R²  - r²) = π(6² - 5²) = 11π (m²)

👉 Luyện chủ điểm: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

2.4. Bài toán vị trí tương đối của đường thẳng và đường tròn

Bài toán 1: Cho đường thẳng a và điểm O cách a một khoảng bằng 5 cm. Không vẽ hình, hãy dự đoán xem mỗi đường tròn sau cắt, tiếp xúc hay không cắt đường thẳng a. Tại sao?

a) (O; 3 cm)

b) (O; 7 cm)

c) (O; 5 cm)

Hướng dẫn giải

a) (O; 3 cm)

Vì 3 cm < 5 cm nên R < d suy ra đường tròn (O; 3 cm) không cắt đường thẳng a.

b) (O; 7 cm) 

Vì 7 cm > 5 cm nên R > d suy ra đường tròn (O; 7 cm) cắt đường thẳng a.

c) (O; 5 cm) 

Vì R = d = 5 cm nên đường tròn (O; 5 cm) tiếp xúc với đường thẳng a.

Bài toán 2: Cho ∆ ABC có đường cao AH. Chứng minh BC là tiếp tuyến của (A; AH)

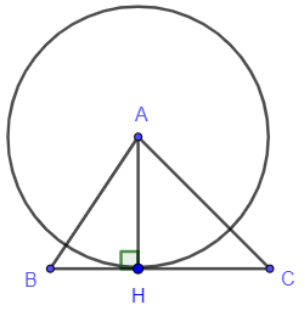
Hướng dẫn giải

Ta có:

• H (A; AH)
• H BC
• BC ⊥ AH = {H}

Suy ra BC là tiếp tuyến của (A; AH)

Bài toán 3: Cho (O) và điểm A nằm ngoài đường tròn, qua A kẻ hai tiếp tuyến AB và AC của (O) với B, C là tiếp điểm. Chứng minh rằng AO là đường trung trực của đoạn thẳng BC.

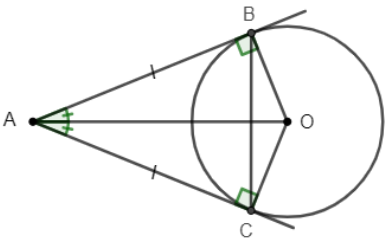
Hướng dẫn giải

Do AB, AC là hai tiếp tuyến của (O) nên AB = AC và AO là tia phân giác của góc BAC.

Xét tam giác ABC có AB = AC nên tam giác ABC là tam giác cân tại A, có AO là tia phân giác của góc BAC nên AO đồng thời là đường trung trực của BC (đpcm).

👉 Luyện chủ điểm: Vị trí tương đối của đường thẳng và đường tròn

2.5. Bài toán vị trí tương đối của hai đường tròn

Bài toán 1: Cho hai điểm O và O’ sao cho OO’ = 6 cm. Hãy giải thích tại sao hai đường tròn (O; 4 cm) và (O’; 3 cm) cắt nhau.

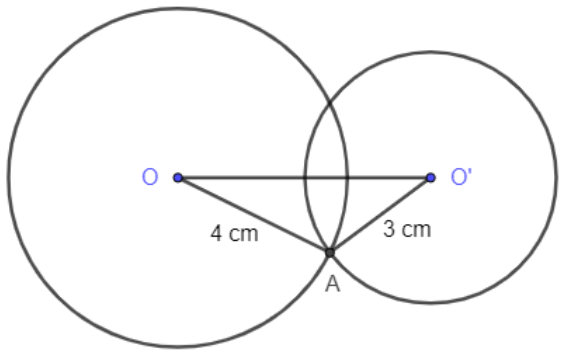
Hướng dẫn giải

Đặt R = 4 cm; R’ = 3 cm;

Ta thấy: 4 cm - 3 cm < 6 cm < 4 cm + 3 cm;

Nên: R - R’ < OO’ < R + R’;

Do đó hai đường tròn đã cho cắt nhau.

Bài toán 2: Cho hai điểm O và O’ sao cho OO’ = 5 cm. Hãy giải thích tại sao hai đường tròn (O; 3 cm) và (O’; 2 cm) tiếp xúc nhau. Chúng tiếp xúc trong hay tiếp xúc ngoài?

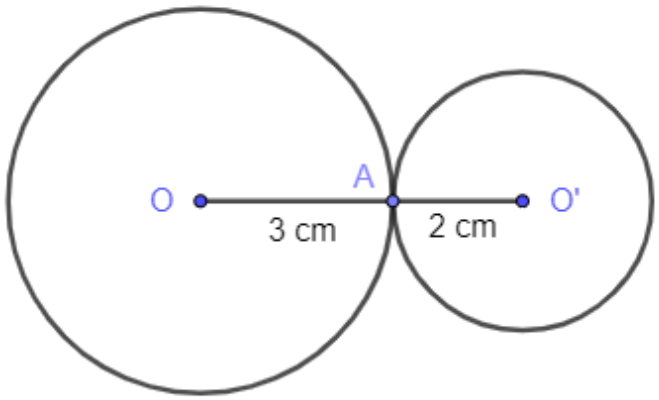
Hướng dẫn giải

Đặt R = 3 cm; R’ = 2 cm;

Ta thấy: 5 cm = 3 cm + 2 cm;

Nghĩa là: OO’ = R + R’;

Vậy hai đường tròn đã cho tiếp xúc ngoài với nhau.

Bài toán 3: Xác định vị trí tương đối của hai đường tròn (O; 3 cm) và (O’; 4 cm), biết rằng OO’ > 7 cm.

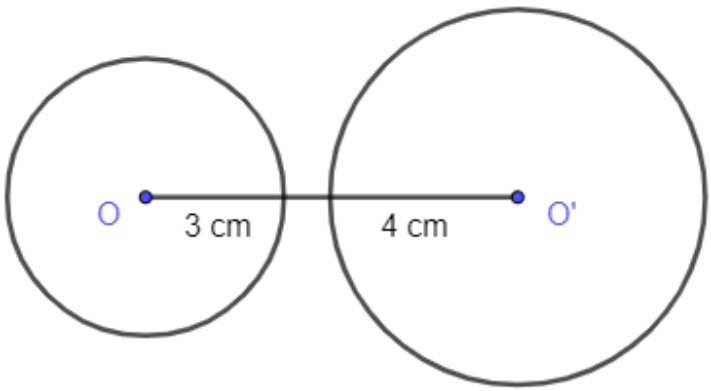
Hướng dẫn giải

Đặt R = 3 cm; R’ = 4 cm;

Ta có: OO’ > 7 cm = R + R’;

Vậy (O; 3 cm) và (O’; 4 cm) là hai đường tròn ngoài nhau.

👉 Luyện chủ điểm: Vị trí tương đối của hai đường tròn

3. Tổng hợp bài tập đường tròn lớp 9 học kì 2

3.1. Bài toán góc nội tiếp

Bài toán: Cho (O; OA) và các điểm như hình dưới. Tính góc CAB, góc ABC, góc COB.

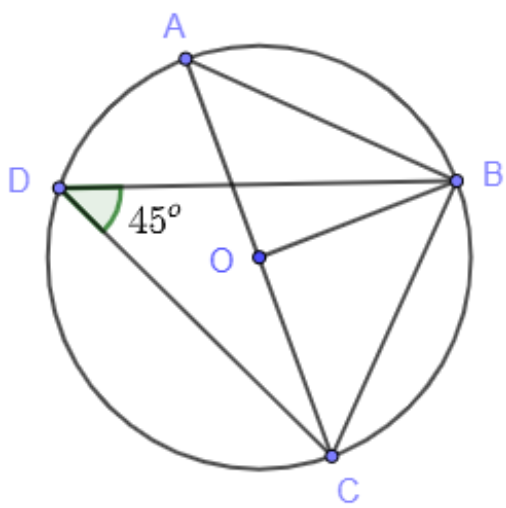
Hướng dẫn giải

• Xét 2 góc nội tiếp ∠CDB và ∠BAC cùng chắn cung BC nên:

∠CDB = ∠BAC = 45^o

• Do góc ABC là góc nội tiếp chắn nửa đường tròn nên:

∠ABC = 90^o

• Do góc nội tiếp ∠CDB và góc ở tâm ∠COB cùng chắn cung BC nên:

∠COB = 2.∠CDB = 2.45^o = 90^o

👉 Luyện chủ điểm: Góc nội tiếp

3.2. Bài toán đường tròn ngoại tiếp và đường tròn nội tiếp

Bài toán 1: Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Tính bán kính đường tròn (O) ngoại tiếp tam giác ABC.

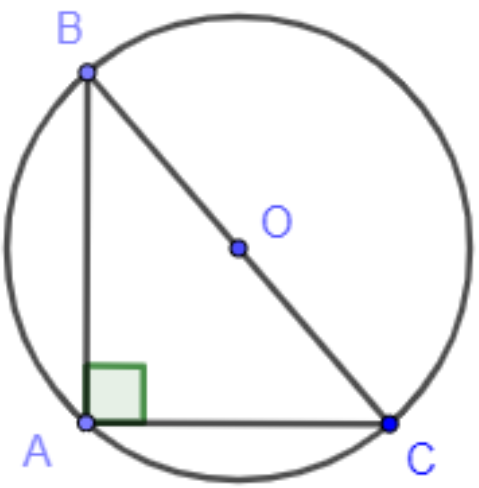
Hướng dẫn giải

Ta có: 6² + 8² = 10² hay AB² + AC² = BC²

Nên theo định lí Pythagore đảo suy ra ∆ ABC vuông tại A.

Khi đó bán kính đường tròn (O) ngoại tiếp ∆ ABC là:

BO = OC = BC/2 = 10/2 = 5 (cm)

Bài toán 2: Cho tam giác đều ABC có cạnh bằng 5 cm. Tính bán đường tròn ngoại tiếp tam giác ABC.

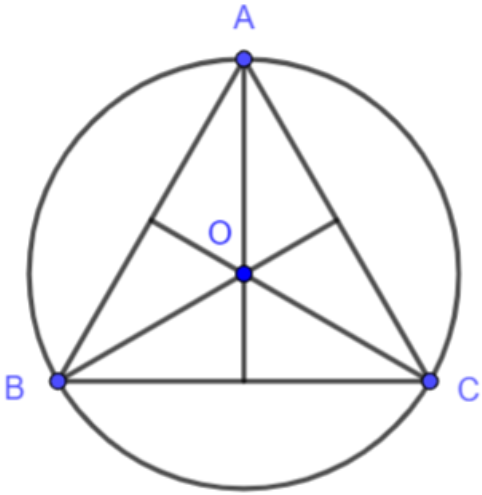
Hướng dẫn giải

Gọi (O; R) là đường tròn ngoại tiếp ∆ ABC.

Do tam giác ABC là tam giác đều nên O sẽ là trọng tâm của ∆ ABC và bán kính đường tròn (O) là:

R = OA = OB = OC = √3/3.5 = 5√3/3 (cm)

Bài toán 3: Cho tam giác đều ABC.

a) Vẽ đường tròn (I, r) nội tiếp tam giác ABC.

b) Biết BC = 6 cm. Hãy tính bán kính r.

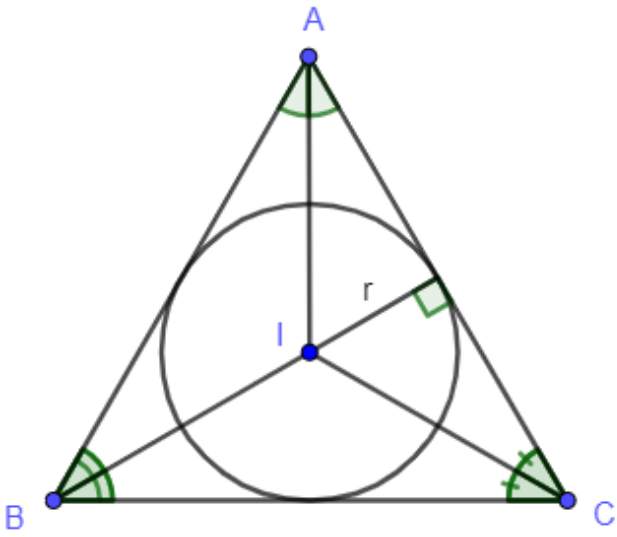
Hướng dẫn giải

a) Vẽ đường tròn (I, r) nội tiếp tam giác ABC

Vẽ 3 đường phân giác trong của 3 góc A, B, C.

Ba đường phân giác cắt nhau tại I. Đo khoảng cách r từ I đến 1 cạnh của ∆ ABC rồi ta vẽ đường tròn (I, r).

b) Biết BC = 6 cm. Hãy tính bán kính r

Bán kính r = √3/6.6 = √3 (cm)

👉 Luyện chủ điểm: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác

3.3. Bài toán tứ giác nội tiếp

Bài toán 1: Cho ∆ ABC có các đường cao BE, CF. Biết góc BCE bằng 40^o.

a) Chứng minh tứ giác BCEF nội tiếp đường tròn có tâm là trung điểm cạnh BC.

b) Tính số đo góc BFE.

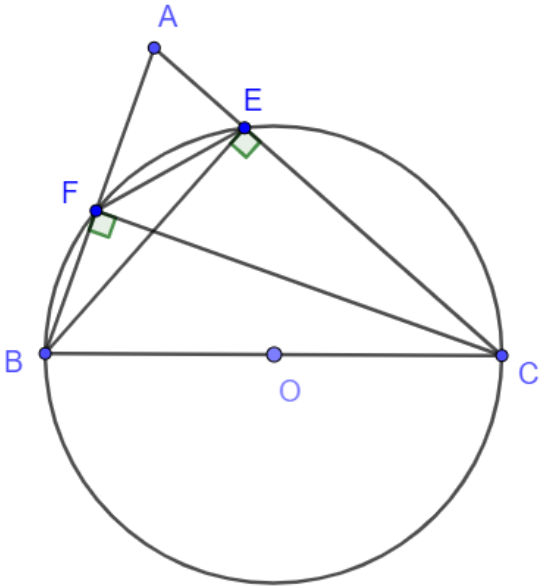
Hướng dẫn giải

a) Chứng minh tứ giác BCEF nội tiếp đường tròn có tâm là trung điểm cạnh BC

Gọi O là trung điểm BC. Do ∆ BCE, ∆ BCF vuông và có chung cạnh huyền BC nên OE = OB = OC = OF.

Vậy tứ giác BCEF nội tiếp đường tròn (O, OB).

b) Tính số đo góc BFE

Do tổng các góc đối nhau của tứ giác nội tiếp BCEF bằng 180 nên:

∠BFE = 180^o - ∠BCE = 180^o - 140^o = 140^o

Bài toán 2: Cho hình chữ nhật ABCD có AB = 6 cm, AD = 8 cm. Vẽ đường tròn (O; R) ngoại tiếp hình chữ nhật ABCD và tính bán kính R.

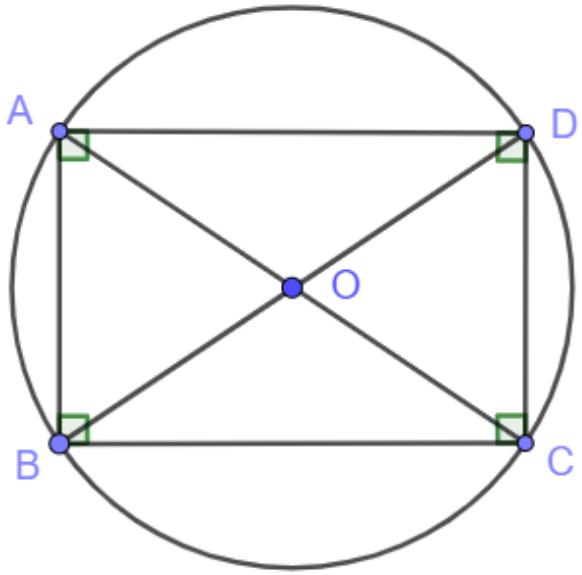
Hướng dẫn giải

Gọi O là giao điểm của AC và BD. Vẽ đường tròn tâm O bán kính R = OA. Đường tròn (O; R) vừa vẽ ngoại tiếp hình chữ nhật ABCD.

Áp dụng định lí Pythagore cho ∆ ABD vuông tại A, ta có:

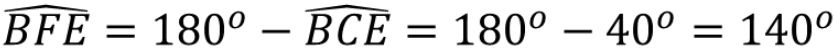
Do đó, ta có R = BD : 2 = 10 : 2 = 5 (cm)

👉 Luyện chủ điểm: Tứ giác nội tiếp

3.4. Bài toán đa giác đều

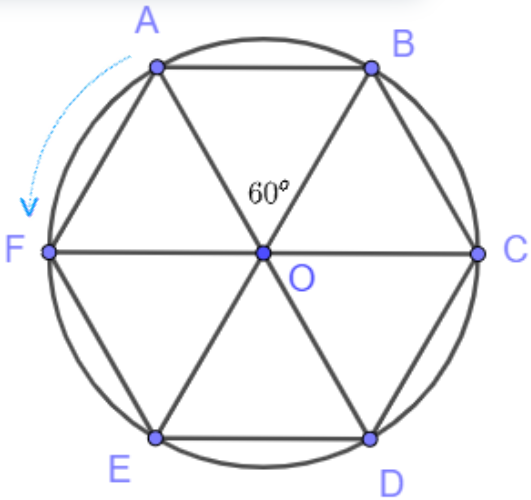
Bài toán 1: Cho lục giác đều ABCDEF nội tiếp (O). Hãy cho biết các phép quay ngược chiều 60°, 120°, 180°, 240° với tâm O biến điểm A thành những điểm nào?

Hướng dẫn giải

Do lục giác ABCDEF đều nên các cung nhỏ AB, BC, CD, DE, EF, FA bằng nhau và bằng: 360° : 6 = 60°.

Khi đó:

- Phép quay ngược chiều 60° biến điểm A thành điểm F

- Phép quay ngược chiều 120° biến điểm A thành điểm E

- Phép quay ngược chiều 180° biến điểm A thành điểm D

- Phép quay ngược chiều 240° biến điểm A thành điểm C

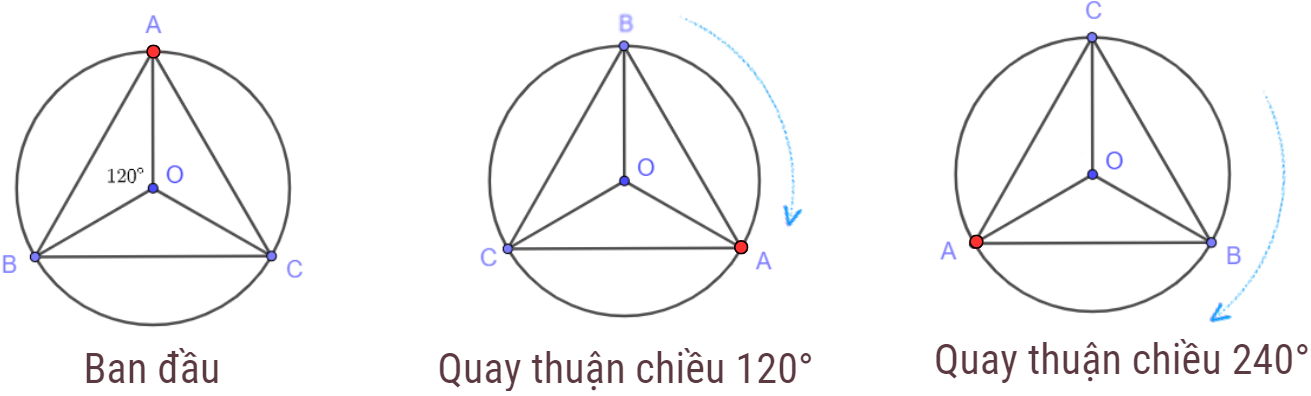
Bài toán 2: Cho ∆ ABC đều nội tiếp (O). Biểu diễn 2 phép quay giữ nguyên ∆ ABC.

Hướng dẫn giải

Do ∆ ABC đều nên các cung nhỏ AB, BC, CA bằng nhau và bằng: 360° : 3 = 120°

Khi đó ta biểu diễn 2 phép quay thuận chiều là 120° và 240° với tâm O.

👉 Luyện chủ điểm: Đa giác đều

4. Một số dạng bài tập đường tròn lớp 9 nâng cao

Dạng 1: Mô hình hai tiếp tuyến cắt nhau

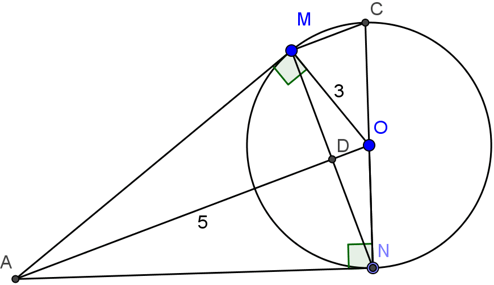
Bài 1: Cho đường tròn (O), điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm).

a) Chứng minh rằng OA ⊥ MN

b) Vẽ đường kính NOC. Chứng minh rằng MC // AO

c) Tính độ dài các cạnh của tam giác AMN biết QM = 3cm, OA = 5cm

Hướng dẫn giải

a) Chứng minh rằng OA ⊥ MN

Ta có:

AM = AN (theo tính chất của 2 tiếp tuyến cắt nhau)

Mà OM = ON (vì cùng bằng R)

Suy ra AO là đường trung trực của MN

Suy ra OA ⊥ MN

b) Chứng minh rằng MC // AO

Xét tam giác MNC có: NC là đường kính nên suy ra góc NMC = 90^o

=> NM ⊥ MC

Mà OA ⊥ MN (chứng minh trên)

Suy ra MC // OA

c) Tính độ dài các cạnh của tam giác AMN

Xét tam giác vuông AMO. Theo định lý Py-ta-go ta có:

AM = √(AO² - OM²) (cm) = 4(cm)

Vì AM = AN nên AN = 4cm

Ta có: OA ⊥ MN (chứng minh trên)

Xét tam giác vuông AMO. Theo hệ thức lượng trong tam giác vuông ta có:

AO.MD = AM.MO

5.MD = 4.3

Suy ra MD = 12/5

Vì MN = 2MD = 2.12/5 = 24/5 (cm)

Vậy AM = AN = 4cm; MN = 24/5 cm.

Bài 2: Cho đường tròn (O), điểm M nằm bên ngoài đường tròn. Kẻ tiếp tuyến MD, ME với đường tròn (D, E là các tiếp điểm). Qua điểm I thuộc cung nhỏ DE, kẻ tiếp tuyến với đường tròn, cắt MD và ME theo thứ tự ở P và Q. Biết MD = 4cm, tính chu vi tam giác MPQ.

Hướng dẫn giải

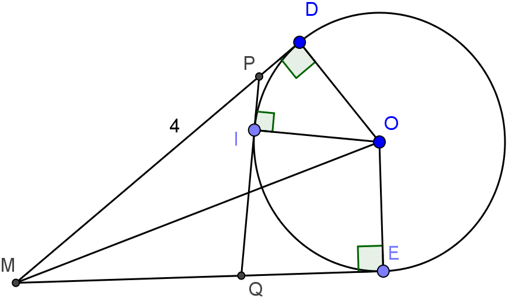
Ta có:

+ PD và PI là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại P

Suy ra PD = PI

+ QI và QE là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại Q

Suy ra QI = QE

+ MD và ME là hai tiếp tuyến của đường tròn tâm (O) cắt nhau tại M

Suy ra MD = ME

Chu vi tam giác MPQ là: MP + PQ + MQ

= MD- PD + PI + IQ + ME - QE

= MD - PI + PI + QE + MD - QE

= 2MD = 2.4 = 8(cm)

Vậy chu vi tam giác MPQ là 8cm.

👉 Luyện chủ điểm: Mô hình hai tiếp tuyến cắt nhau

Dạng 2: Mô hình tam giác nội tiếp đường tròn

Bài toán: Cho tam giác nhọn ABC (AB < AC) nội tiếp trong đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh tứ giác AEHF nội tiếp

b) Chứng minh OA vuông góc EF

Hướng dẫn giải

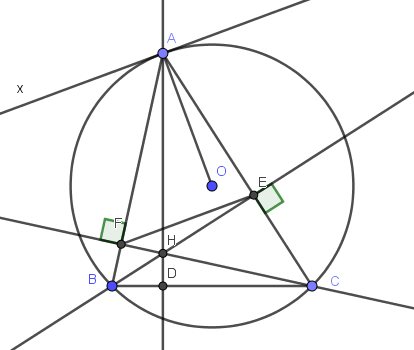
a) Chứng minh tứ giác AEHF nội tiếp

Vì $AD,BE,CF$ là đường cao của tam giác $ABC$ và cắt nhau tại $H$ nên

Tứ giác $AEHF$ có tổng hai góc đối nhau 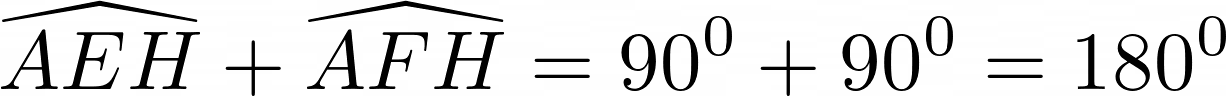nên $AEHF$ là tứ giác nội tiếp.

b) Chứng minh OA vuông góc EF

Kẻ tiếp tuyến $Ax$ của $(O)$. Ta có $OA\perp Ax(1)$

$(2)$ (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó - cung $AB$)

Tứ giác $BFEC$ có và cùng nhìn cạnh $BC$ nên $BFEC$ là tứ giác nội tiếp.

$(3)$

Từ (2), (3) 

Mà 2 góc này ở vị trí so le trong nên $Ax\; //EF(4)$

Từ $=>OA\perp EF$

👉 $Luyện\; chủ\; điểm:\; Mô\; hình\; tam\; giác\; nội\; tiếp\; đường\; tròn$

Dạng 3: Mô hình hai đường tròn cắt nhau

Bài toán: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung tại A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE.

a) Tứ giác AMIN là hình gì? Vì sao?

b) Chứng minh hệ thức IM.IO = IN.IO’.

c) Chứng minh rằng OO’ là tiếp tuyến của đường tròn có đường kính là DE.

d) Tính độ dài DE biết rằng OA = 5cm, O’A = 3,2cm.

Hướng dẫn giải

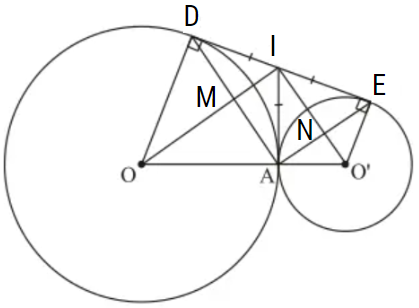
a) Tứ giác AMIN là hình gì? Vì sao?

Trong đường tròn (O) ta có OI là tia phân giác của góc AID ( tính chất hai tiếp tuyến cắt nhau)

Trong đường tròn (O’) ta có O’I là tia phân giác của góc AIE (tính chất hai tiếp tuyến cắt nhau)

=> IO ⊥ IO’ ( tính chất kề bù)

Suy ra: 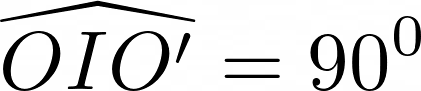hay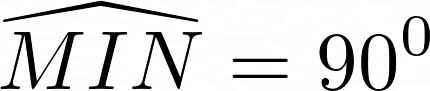

Lại có: IA = ID (tính chất hai tiếp tuyến cắt nhau)

Suy ra tam giác ADI có IO là phân giác của góc AID nên IO cũng là đường cao của tam giác AID.

Suy ra: IO ⊥ AD hay góc AMI = 90⁰

Mặt khác: IA = IE (tính chất hai tiếp tuyến cắt nhau)

Suy ra tam giác AEI cân tại I.

Tam giác cân AIE có IO’ là phân giác của góc AIE nên IO cũng là đường cao của tam giác AIE.

Suy ra: IO’ ⊥ AE hay góc ANI = 90⁰

Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật.

b) Chứng minh hệ thức IM.IO = IN.IO’

Tam giác AIO vuông tại A có AM ⊥ IO.

Theo hệ thức lượng trong tam giác vuông, ta có:  IA² = IM.IO      (1)

Tam giác AIO’ vuông tại A có AN ⊥ IO’.

Theo hệ thức lượng trong tam giác vuông, ta có: IA² = IN.IO’      (2)

Từ (1) và (2) suy ra: IM.IO = IN.IO’

c) Chứng minh rằng OO’ là tiếp tuyến của đường tròn có đường kính là DE

Ta có: IA = ID = IE ( chứng minh trên)

Suy ra A nằm trên đường tròn tâm I đường kính DE.

Vì OO’ ⊥ IA tại A nên OO’ là tiếp tuyến của đường tròn tâm I, bán kính DE/2.

d) Tính độ dài DE

Tam giác O’IO vuông tại I có IA ⊥ OO’.

Theo hệ thức lượng trong tam giác vuông, ta có:

IA² = OA.O’A = 5.3,2 = 16

Suy ra: IA = 4 (cm).

Mà DE = 2IA nên DE = 2.4 = 8 (cm)

👉 Luyện chủ điểm: Mô hình hai đường tròn cắt nhau

Dạng 4: Mô hình nửa đường tròn

Bài toán: Cho nửa đường tròn (O) đường kính AB. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax và By. Điểm M nằm trên (O) sao cho tiếp tuyến tại M cắt Ax, By tại C và D.

a) Chứng minh: AC + BD = CD

b) Chứng minh: Góc COD = 90⁰

c) Chứng minh: AC.BD = OA²

Hướng dẫn giải

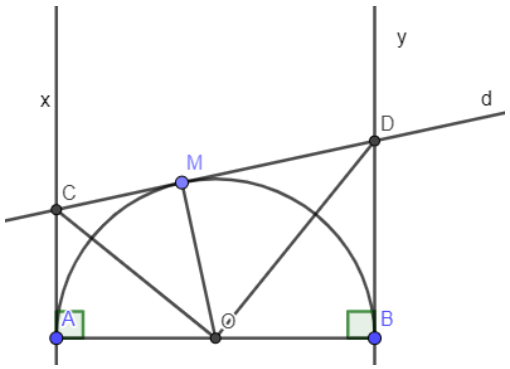
a) Chứng minh: AC + BD = CD

Gọi d là tiếp tuyến của (O) qua M

Vì Ax và d là hai tiếp tuyến cắt nhau tại C => AC = CM (tính chất) (1)

Vì By và d là hai tiếp tuyến cắt nhau tại D => BD = DM (tính chất) (2)

Cộng vế với vế của (1) và (2) ta được:

AC + BD = CM + DM

=> AC + BD = CD (điều phải chứng minh).

b) Chứng minh: Góc COD = 90⁰

Vì Ax và d là hai tiếp tuyến cắt nhau tại C => góc AOC = góc MOC

Vì By và d là hai tiếp tuyến cắt nhau tại D => góc MOD = góc BOD

Ta có:

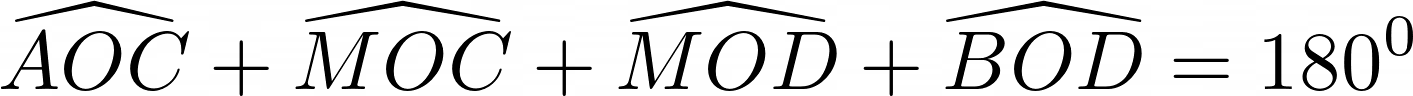
Mà: Mà góc AOC = góc MOC và góc MOD = góc BOD

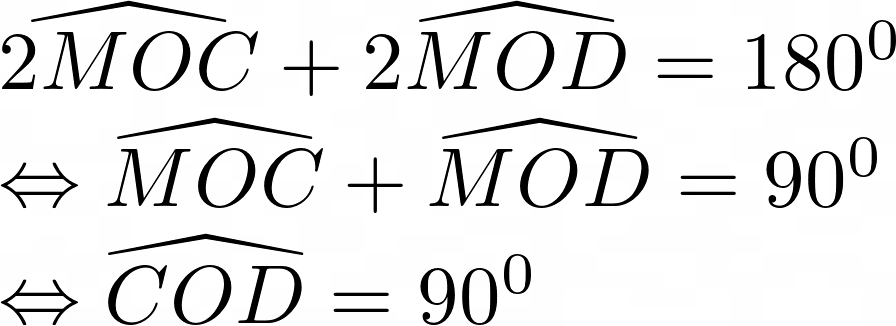
c) Chứng minh: AC.BD = OA²

Vì d là tiếp tuyến của (O) tại M nên CD là tiếp tuyến của (O) tại M

Do đó: CD ⊥ OM tại M

Xét tam giác COD vuông tại O có OM là đường cao ta có:

OM² = CM.DM (hệ thức lượng trong tam giác vuông)

Ta có:

OM = OA (bán kính)

CM = CA (cmt)

BM = BD (cmt)

Do đó: OM² = CM.DM <=> OA² = CA.BD

=> CA.BD = R² (do OA = R).

👉 Luyện chủ điểm: Bài tập mô hình nửa đường tròn

Như vậy, bài viết trên đã giới thiệu đầy đủ kiến thức cần nhớ và các bài tập đường tròn lớp 9. Nắm chắc nội dung kiến thức trên chắc chắn sẽ giúp ích cho các em học sinh đang trong quá trình ôn luyện toán vào 10.

[%Included.TAK12%]